Day 58 in Mat229

• The dot product ${\overline{u}}\cdot{\overline{v}}$ is a scalar product (produces a number). The number reflects the extent to which the two vectors ${\overline{u}}$ and ${\overline{v}}$ are aligned or not. In particular, the dot product is 0 when two vectors point in perpendicular directions. Thus it provides a test for perpendicularity.

  It also is used to compute the length of a vector: \[ |{\overline{u}}|=\sqrt{{\overline{u}}\cdot{\overline{u}}} \]

  Finally, the dot product provides a means for computing the angle $\theta$ formed between two vectors when their butt ends are located at the same point:

  

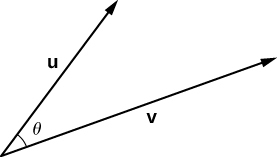
  \[ {\overline{u}}\cdot{\overline{v}} = |{\overline{u}}||{\overline{v}}|\cos(\theta) \]

  If we know the components of the vectors, e.g. ${\overline{u}}=\langle u_1,u_2,\ldots,u_n\rangle$ for the $n$-dimensional vector, then its easy to compute the dot product of two vectors: \[ {\overline{u}}\cdot{\overline{v}} = \sum_{i=1}^n u_i v_i \]

• The cross product ${\overline{u}}\times{\overline{v}}$ is a vector product (produces a vector) -- but only works in three-dimensions. Its magnitude reflects the extent to which the two vectors ${\overline{u}}$ and ${\overline{v}}$ are parallel. In particular, the cross product has 0 length when two vectors point in parallel directions. Thus it provides a test for parallelness (but only in three dimensions!).

  It also is used to compute the area of a parallelogram formed by putting the butts of the two vectors together: \[ |{\overline{u}}\times{\overline{v}}|=|{\overline{u}}||{\overline{v}}| \sin(\theta) \]

  where \(\theta \in [0,\pi]\) (thus \(\sin(\theta) \ge 0\)).

  Notice that the parallelogram has zero area when the vectors are parallel, and maximal area when the vectors are perpendicular.

  Finally, the cross product provides a means for producing a vector perpendicular to both ${\overline{u}}$ and ${\overline{v}}$ -- so enables us to "leap from a plane", as it were, the plane in which that parallelogram, formed by putting the butts of the two vectors together, lives.

  

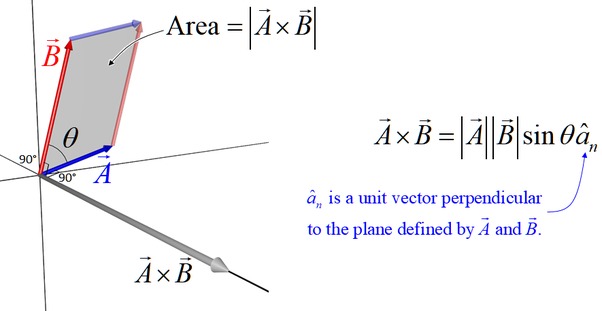
  Since I borrowed this image I shouldn't be too critical, but it's important to note that the unit vector mentioned, $\hat{a}_n$, is the unit vector chosen by the right-hand rule (more about that in the materials below). I believe that the use of the subscript "$n$" on that unit vector indicates "normal" -- that is, perpendicular -- to the plane.

• Materials:
  • Vector Products (.pdf)
  • Vector Products (.nb)

Background information:

In the first four pages of your handout today you'll find a description of some of the elements of calculus applied to "space curves" -- motions represented by vectors. The magnitude is typically distance, and the direction is taken from a given origin. In our case, the distance and direction of a planet from the sun.

1. Page 1: the limit definition of the derivative still works! And we derive velocity and acceleration in "the usual ways".

   Note also the simplifying assumption: ignore all but the planet and the sun.

2. Page 2, Example 1: position vectors and motions in 2D
3. Page 2, Example 2: Works in 3D, too!
4. Page 2, Example 3: Integration works, too! Just more work to do, depending on the dimension.
5. Page 3, Example 4: uniform circular motion and centripetal force.
6. Page 3, Example 5: projectile motion in the plane, and components as parametric equations

• Page 1: Kepler's three laws, and setting up our coordinate system; Newton's Second law of motion.
• Page 2: Newton's law of universal gravitation (an "inverse square" law), \[ \overline{F}=-\frac{GMm}{r^3}\overline{r}=-\frac{GMm}{r^2}\hat{u} \] where \(\hat{u}\) is the unit vector in the \(\overline{r}\) direction. Thus he proposed a "center-seeking" force (of gravity).

1. Equate \[ \overline{F}=m\overline{a} = -\frac{GMm}{r^2}\hat{u} \] to get \[ \overline{a} = -\frac{GM}{r^2}\hat{u} \]

2. Knowing what we do about the cross product, since \(\overline{a}\) and \(\overline{r}\) are parallel,

   \[ \overline{r} \times \overline{a} = \overline{0} \] Note, by the way, that the result is the zero vector; it's 0 in every component.

3. We're now going to use result 2: compute the following derivative with respect to time, using a product rule (just have to trust us on this!:), \[ \frac{d}{dt}\left(\overline{r} \times \overline{v}\right) = \overline{r}^\prime \times \overline{v} + \overline{r} \times \overline{v}^\prime = \overline{v} \times \overline{v} + \overline{r} \times \overline{a} = \overline{0} \]

4. Since the derivative (in time) of this vector quantity is \(\overline{0}\), \[ \overline{r} \times \overline{v} = \overline{h} \] with \(\overline{h}\) a constant vector, perpendicular to both \(\overline{r}\) and \(\overline{v}\) for all values of time \(t\).

   This means that the motion occurs entirely in the plane to which \(\overline{h}\) is perpendicular.

5. Recall from the cross product's definition that the magnitude of \(\overline{h}\) is the area of the parallelogram created by the vectors \(\overline{r}\) and \(\overline{v}\).

   This tells us that \[ |\overline{r}(\theta(t))||\overline{v}(\theta(t))|\sin(\theta(t)) \] is constant in time. (This will come up in the Mathematica file to create planetary motion consistent with the path of the planet.)

6. A second product rule for derivatives appears in the next calculation, for \(\overline{h}\): \[ \overline{h} = \overline{r} \times \overline{v} = \overline{r} \times \overline{r}^\prime = r\hat{u} \times \left(r\hat{u}\right)^\prime = r\hat{u} \times \left(r^\prime \hat{u} + r\hat{u}^\prime\right) = r^2\hat{u} \times \hat{u}^\prime \] (since \(r\hat{u} \times r^\prime \hat{u} = \overline{0}\)).

   Our objective is to get an expression for \(\overline{v} \times \overline{h}\), so let's go there now:

7. But we'll sneak up on it, by considering \[ \left(\overline{v} \times \overline{h}\right)^\prime = \overline{a} \times \overline{h} = -\frac{GM}{r^2}\hat{u} \times \left(r^2\hat{u} \times \hat{u}^\prime\right) = GM \hat{u}^\prime \] (via some somewhat murky calculations, pages 2-3).

8. And since their derivatives with respect to time are equal, the two quantities differ by only a constant (vector -- call it \(\overline{c}\)): \[ \overline{v} \times \overline{h} = GM \hat{u} + \overline{c} \]

9. These two constant vectors, \(\overline{h}\) and \(\overline{c}\), are mutually perpendicular, and so their directions are chosen as two of the coordinate axes (figure 8, p. 3) in which to study the motion. (Their cross product could serve as the third! In this figure is it \(\overline{h} \times \overline{c}\) or \(\overline{c} \times \overline{h}\))?

   \(\overline{h}\) is perpendicular to the plane of the motion, whereas \(\overline{c}\) is in the plane of the motion. It will turn out that \(\overline{c}\) is closely related to the "eccentricity" of the elliptical orbit, which is defined as \(e = \frac{c}{GM}\), where \(c=|\overline{c}|\).

10. Define \(\theta\) as the angle between the \(\overline{c}\) and \(\overline{r}\) vectors.

    Our goal now is to solve for \(r=f(\theta)\), and hope that it's an ellipse!

    \[ \overline{r} \cdot \left(\overline{v} \times \overline{h}\right) = \overline{r} \cdot \left(GM \hat{u} + \overline{c}\right) = GMr + rc\cos(\theta) = r(GM + c\cos(\theta)) \] But, by a property relating dot and cross products (see your vector products handout, property 3), \[ \overline{r} \cdot \left(\overline{v} \times \overline{h}\right) = \left(\overline{r} \times \overline{v}\right) \cdot \overline{h} = \overline{h} \cdot \overline{h} = h^2 \]

11. Now we solve for \(r\): \[ r = \frac{h^2}{GM + c\cos(\theta)} \] With \(e = \frac{c}{GM}\), and defining \(d = \frac{h^2}{c}\), we can write this as \[ r = \frac{e d}{1 + e\cos(\theta)} \] which is the equation of an ellipse, with the origin at one focus.

12. Thus Kepler's first law is established, derived from Newton's universal rules....

That parallelogram's area is proportional to the area of the ellipse swept out in time.

• The source material for our Kepler study, from Stewart's Calculus.
• Stewart's lead up to our Kepler study.
• Illustrating Kepler's first law: how planets travel in ellipses