- Today we will finish our investigation of three-dimensional
representations of points, planes, and spheres, as well as
vectors (sections Vol
3, Sec 2.1: Vectors in the Plane and Vol 3, Sec 2.2: Vectors in Three Dimensions).
- Then we will study two different types of vector
multiplication: the dot-product, and the
cross-product:
Vol
3, Sec 2.3: The Dot Product and Vol
3, Sec 2.4: The Cross Product.
- Finally Thursday we will end with three-dimensional
parametric curves, and an application to Earth's orbit around
the sun.
- Friday will be a review day.
- We encountered analogues to many of our friends from two dimensions:
- The distance formula generalized
- Planes rather than lines (3-d linear equations)
- Spheres rather than circles
- Materials:
- We consider two products that pertain to vectors:
- The dot product ${\overline{u}}\cdot{\overline{v}}$
is a scalar product (produces a number). The number
reflects the extent to which the two vectors ${\overline{u}}$
and ${\overline{v}}$ are aligned or not. In particular, the dot
product is 0 when two vectors point in perpendicular
directions. Thus it provides a test for
perpendicularity.
It also is used to compute the length of a vector: \[ |{\overline{u}}|=\sqrt{{\overline{u}}\cdot{\overline{u}}} \]
Finally, the dot product provides a means for computing the angle $\theta$ formed between two vectors when their butt ends are located at the same point:
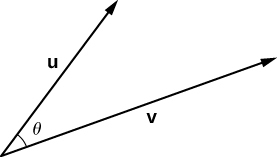
\[ {\overline{u}}\cdot{\overline{v}} = |{\overline{u}}||{\overline{v}}|\cos(\theta) \]
If we know the components of the vectors, e.g. ${\overline{u}}=\langle u_1,u_2,\ldots,u_n\rangle$ for the $n$-dimensional vector, then its easy to compute the dot product of two vectors: \[ {\overline{u}}\cdot{\overline{v}} = \sum_{i=1}^n u_i v_i \]
- The cross product ${\overline{u}}\times{\overline{v}}$ is a
vector product (produces a vector) -- but only works in
three-dimensions. Its magnitude reflects the extent to which the two
vectors ${\overline{u}}$ and ${\overline{v}}$ are parallel. In
particular, the cross product has 0 length when two vectors point in
parallel directions. Thus it provides a test for parallelness
(but only in three dimensions!).
It also is used to compute the area of a parallelogram formed by putting the butts of the two vectors together: \[ |{\overline{u}}\times{\overline{v}}|=|{\overline{u}}||{\overline{v}}| \sin(\theta) \]
where \(\theta \in [0,\pi]\) (thus \(\sin(\theta) \ge 0\)).
Notice that the parallelogram has zero area when the vectors are parallel, and maximal area when the vectors are perpendicular.
Finally, the cross product provides a means for producing a vector perpendicular to both ${\overline{u}}$ and ${\overline{v}}$ -- so enables us to "leap from a plane", as it were, the plane in which that parallelogram, formed by putting the butts of the two vectors together, lives.
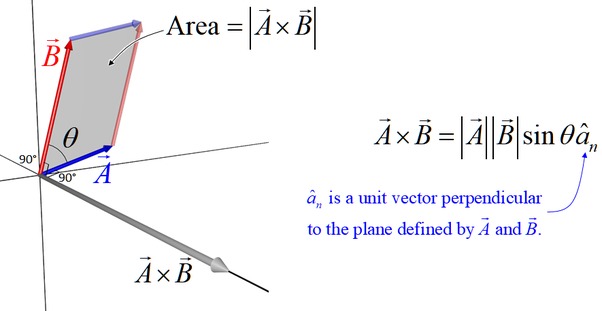
Since I borrowed this image I shouldn't be too critical, but it's important to note that the unit vector mentioned, $\hat{a}_n$, is the unit vector chosen by the right-hand rule (more about that in the materials below). I believe that the use of the subscript "$n$" on that unit vector indicates "normal" -- that is, perpendicular -- to the plane.
- Materials:
- The dot product ${\overline{u}}\cdot{\overline{v}}$
is a scalar product (produces a number). The number
reflects the extent to which the two vectors ${\overline{u}}$
and ${\overline{v}}$ are aligned or not. In particular, the dot
product is 0 when two vectors point in perpendicular
directions. Thus it provides a test for
perpendicularity.
- Links:
- The source material for our Kepler study, from Stewart's Calculus.
- Deriving Kepler's first law: why planets travel in ellipses
- Polar graph paper
- Lab 11 Review worksheet
- Prof. Roger Zarnowski's cool series tools handout
- Wolfram Alpha
- Mathematica on-line is an option, if you are at a computer without Mathematica installed.
Website maintained by Andy Long. Comments appreciated.