This module assumes that you have read or will read the associated articles:
- Webster R., et al. 1994. Kriging the Local Risk of a Rare Disease from a Register of Diagnoses. Geographical Analysis, 26:2, pp. 168-185.
- Carrat, F. and A. Valleron. Epidemiologic Mapping using the 'Kriging' Method: Application to an Influenza-like illness Epidemic in France. American Journal of Epidemiology, 135:11, pp. 1293-1300.
What do we learn from them? They contain a good deal of explanation, some suggested strategies, and a number of rules of thumb. Here's my summary, but you really should do the reading (or read some other good descriptive papers/texts).
First of all, there is much too much to say! This is a field with broad application, and a myriad of techniques. We'll only be getting into the basics, of course.
Geostatistical models are used essentially for (at least) three reasons:
- to characterize (i.e. model) spatial autocorrelation (via the variogram),
- to create continuous maps based on the data for an area (via kriging), and
- to simulate realizations (data sets) based on a given variogram model.
Geostatistics is useful in moving from the data to thematic maps, in the analysis of spatial autocorrelation, and in creating maps for visualization and ESDA.
There are many, many different ways to make maps. Some methods are better than others, of course, and we want to focus today on a couple of techniques which allow for the production of maps that are optimal (in a sense to be described).
You might be asking: If my software package has an option for interpolating, why not just punch a button? Because it's not good science. Yes, it's easy: no argument there; but it's the easy, careless way out. It's certainly a shame to treat important data so cavalierly. At the end of this page is a comparison of two methods that illustrates how different two maps produced from the same data can be. Let's begin by looking at some sample 1-d problems, to get us thinking about how to estimate away from spatial data locations.
"If variograms didn't exist, optimal interpolation would require that they be invented...." The unknown quotesman. Usually folks start with the variogram and get to the kriging equations; we'll do it slightly differently: we motivate the definition of the variogram via the kriging equations.
We will now derive the kriging equations, thereby accomplishing three objectives:
- The assumptions required (the "intrinsic hypothesis") will become apparent;
- the definition of the variogram will fall out naturally; and
- you will get to see how the kriging equations come about.
Variography is the exploration of the spatial autocorrelation of a variable by means of the variogram. Here are some one-dimensional examples, in which the data "function" (on top) gives rise to the variogram (on the bottom):
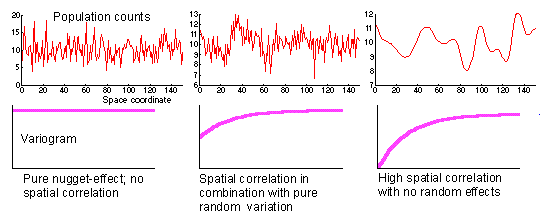
Imagine that we have obtained data samples from the functions above.
- In the lefthand case, we have data which exhibits no spatial autocorrelation, and hence results in a flat variogram;
- in the center case, we see some local noise (big movement on a short scale) over a global (slowly varying) structure, giving rise to a variogram which is lower around zero and climbing, but starting from a positive y-intercept;
- in the righthand case, there is no local noise, so the variogram has a 0 y-intercept. We'll talk more about these characteristics below.
- definition of the variogram
The sample variogram is a spatial decomposition or partition of the sample variance, as described in another module, exploratory spatial data analysis. This leads to my favorite characterization of the variogram, as follows: I think of the variogram as the "trust function". If it is relatively small at a particular lag, then you might assume that points found at that lag from a given position are more similar than points found at distances/angles where the variogram is large.
The variogram allows us to investigate the spatial scale at which the phenomenon under study is spatially autocorrelated. If the variogram is the same at all distances and angles, then there is no spatial autocorrelation for the scale shown. Sampling at smaller scales may show spatial autocorrelation.
- Stationarity
Some degree of stationarity is required for any of this geostatistical analysis to be valid. We might think of our spatially defined process as composed of a random variable at each point in space, all identically distributed (but spatially correlated). This is rather restrictive, and more restrictive than we actually need in our analysis. It turns out that we can get by assuming only the "intrinsic hypothesis" (as described in the derivation of the kriging equations above.
- trend/drift
The drift is a deterministic component underlying spatially autocorrelated randomness, representing the mean surface of the random variable. The ordinary kriging equations are derived assuming a constant mean. It is possible to assume a more complicated mean surface (a constant mean just assumes a flat mean - one might have a mean which is increasing linearly in an area, for example).
If we're in two dimensions, then the trend is a function of x and y, and needs to be removed - or at least accounted for - before we model the variogram. This is something of a Catch-22 situation, as you need to know the trend before doing your variogram analysis. It is possible, however, to create an iterative procedure between variogram analysis and kriging which iterates toward a drift term and the variogram of the residuals.
- computations
Variogram values are usually only presented for distances up to half the "diameter" of the data: we don't show variogram values for the longest pair differences.
Variograms are calculated for many distance classes, and usually for many different angle classes so that we may check for a directional component.
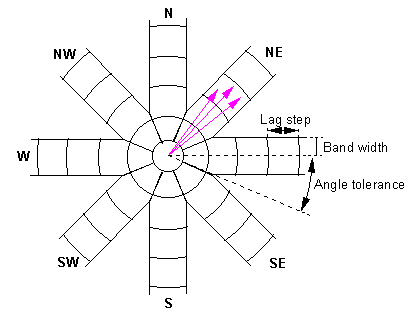
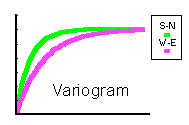
If the variograms appear to be the same in all directions, then we feel justified in taking an isotropic (or omni-directional) model (where we effectively worry only about the distance between points, neglecting their direction). This is an important part of the modelling process.
Only one type of anisotropy is easily dealt with: if the field has an ellipsoidally shaped variogram, we can easily correct for it:

- valid models
- The class of valid models: conditionally
negative definite (CND) functions, including
- linear,
- Power models (more generally): e.g. power (concave down) and power (concave up).
- spherical,
- exponential,
- nugget,
- gaussian
- positive linear combinations of models (that is, sums of models with positive coefficients) are admissible. Thus most realistic models created from real data will contain a nugget effect plus one of the models described above.
- typical model parameters and their
interpretations:
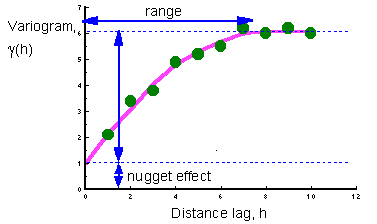
- nugget - the nugget may tell indicate how much noise there is in the data, or the extent to which sampling has not been carried out at the smallest distance scales (lags);
- sill - the sill measures the component of variance of a model; the total sill is the sum of all sills in the models, including the white noise (nugget) component.
- range - the range quantifies the distance over which data are correlated;
- The class of valid models: conditionally
negative definite (CND) functions, including
- Relationship of the variogram to other measures
The variogram is closely related to other, similar measures of spatial autocorrelation (e.g. Moran's I and the correlogram). It is more closely related to Geary's C, however, as described in "Local spatial statistics: an overview", by A. Getis and J. K. Ord (pp. 261-277 in Spatial Analysis: Modelling in a GIS Environment, Longley, P. and M. Batty, eds.
We can consider both the correlogram and the variogram as global, multiple distance measures of spatial autocorrelation, whereas Moran's I and Geary's C are the corresponding global, single distance measures.
- Multivariate generalization
We can create a matrix variogram, consisting of variograms on its diagonal and cross-variograms off the diagonal. Unfortunately, modelling the cross-variograms is really a heavy cross to bear indeed! The variogram matrix must satisfy the Cauchy-Schwartz inequality in each pair of variables and in total.
- When data are non-normal...
Obviously it is the case that extreme values of the distribution of variable values will have a strong effect on the form of the variogram (creating large squared differences).
Geostatisticians tend to try one of two things in this event: either a power or log transformation of the data, or an indicator transformation (described below, under kriging).
- properties
- BLUE:
Best Linear Unbiased Estimator: Kriging is derived so as to be BLUE - interpolator
Kriging generates an interpolating surface to the data (i.e., the surface passes through the data).The nugget plays an important role in this characteristic: if one chooses a variogram model without a nugget, then the interpolation will be smooth: that is, for points in the neighborhood of a data point, the values of the estimate will tend toward the data variable value as we tend toward the data location. With a non-zero nugget, however, this is no longer true: kriging still yields an interpolator, but it is a "jump interpolator" - smooth all around the data values, but making jumps up to data to satisfy its role as an interpolator of the data.
- BLUE:
- types
- global
Global kriging results in a function - the problem is that the linear system to solve is often too ill-conditioned, and may lead to ridiculous - rather than fantastic - results. - local
In local kriging, we only use neighbors within a fixed radius of the position at which an estimate is desired; we may also restrict the number of neighbors used to some fixed (relatively small) number, so as to keep the linear systems small. This makes sense especially when the range is small relative to the scale of the data (points outside of the range aren't really informative, so why use them in the estimation?). - universal
Accounting for drift can be done in an iterative manner, using a variation of kriging called universal kriging; we model the variogram from the data, then use universal kriging which estimates the drift (mean surface) in terms of a basis of functions we provide. Subtract this drift term from the data, then iterate! Eventually we have a deterministic drift term given as a sum of successive drift terms, and a stochastic term which represents a spatially autocorrelated field but without drift (constant mean). Ordinary kriging is the special case of using only one function, a constantThis is related to trend surface analysis, only we let the estimator compute the trend at the same time as it computes the estimates. This suggests an iterative procedure:
- we compute the variogram assuming stationarity;
- krig, and estimate the drift;
- subtract the drift surface from the data, and iterate.
- indicator
Indicator kriging is especially useful when data is horribly non-normal: we transform the data into quartiles or deciles, say, and then krig levels (after modelling the variograms of each of the levels). I'll let University of Michigan geostatistician Pierre Goovaerts describe it. - cokriging - multivariate kriging
If you want to really go crazy (perhaps literally), you might want to look into cokriging, the multivariate version of kriging. The idea is this: suppose that you are interested in mining several minerals (e.g. gold and silver). It may be that the presence of silver implies the presence of gold. Thus, silver might be used as a surrogate for the presence of gold.When it comes time to create the maps for silver and gold in the region to be mined, it may be that the map of silver can be used to enhance the map of gold, and vice versa. In fact, it makes more sense to estimate the two variables simultaneously, resulting in better maps than one would get individually.
To do this mutual estimation in a geostatistical framework, we need to model not just the individual variograms, but also the cross-variograms of each pair of variables (the cross-variogram is the spatial decomposition of the sample covariance). Cross-variogram modelling is generally much harder than variogram modelling, and the estimation procedures just get more unstable (because the matrices just get bigger, and the modelling may lead to non-invertible or nearly-non-invertible matrices). As far as I'm concerned, it should still be considered an experimental procedure best left to those who are willing to run the risks. (Don't tell my advisor that I said that!)
- simple
assumes known mean; - ordinary
estimates mean (the name comes from the fact that this is the most commonly used form); - point
values are assumed to come from point sources, and point values elsewhere are estimated. - block
estimation of spatial averages, rather than point values. - disjunctive (non-linear), factorial, log normal, etc., etc., perhaps ad nauseum....
- global
- diagnostics
- cross-validation
Cross-validation refers to a process whereby one removes a data point from the data set, and then calculates the estimate using the remaining data. Of course we would like to see these estimates equal the data values, and we examine a scatter plot of data versus estimates to get a quick impression of the quality of our kriging estimates. (If the process doesn't even do a good job of reconstructing the data, what makes us think that it will do any good when it comes time to estimating where there is no data?)Myers summarized the statistics that are usually computed for the cross-validation estimates.
- kriging variance
The kriging estimation variance is the quantity we minimized to obtain the kriging estimates. Provided the variogram model is correct, this is indeed the variance of estimation. But some consider it a mistake to rely too heavily on this (e.g. read what Pierre Goovaerts has to say).Some folks (like the authors of our articles) get terribly excited about the kriging variance. But as Pierre says, "only under peculiar conditions is the kriging variance informative for prediction error and sampling strategy. It will just tell you to take additional samples where the sampling density is low. You don't need geostat for that!"
- cross-validation
- a centre-satellite model
- An example from the Illinois cancer data set, comparing two different methods.
One map-making strategy thus is as follows:
- Is your data normal? Might it need to be transformed? Are there other possibilities (e.g. indicator transform) to answer your question?
- Compute the sample variogram of the appropriate form of the data.
- Model the sample variogram to produce the theoretical variogram (effectivally modelling the spatial autocorrelation in the process). Some of the things we model are the spatial scale over which spatial autocorrelation exists, and the white noise component of the variance in the data.
- "Krig" using the model to create the map; and
- Evaluate the map using cross-validation statistics.
This is useful in the same way that looking at 100 histograms of a normal variable is useful: for gaining some perspective on how much variation there is between identically distributed statistical objects. If you have hypothesized a certain model, then you can simulate other data sets based on that model to compare to your own data: do they fit into the simulation group, or not?
At the University of Michigan we are using GS+ in lab, for our analyses. My own preference is for a piece of software called Geo-EAS, which I had a hand in producing (I ported it to UNIX, where it is now a little different from the DOS version). GS+ is easier for a beginner to use, and slicker, however, so we use that.
