The linearization
can be brought to bear in our regression problem, as follows: we seek a fit to
the data using the model form give by the function f, with parameters
. That is, for a given data location i, we have
Once again our objective is to minimize a sum of squared errors over n data locations:
If we take partials of S with respect to the p parameters, we obtain p equations, such as
We then set them equal to zero and hope to find a global minimum (there is no guarantee).
Suppose that we have an initial guess for the parameters, 
,
and are interested in improving it. The trick to make use of this result to
find an improvement to . Once again, the trick is to use the
linearization, and to use our guess .
We replace 
in the summation by the linearization
of f with respect to the p parameters 
of
:
Then
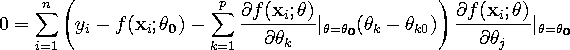
There are p equations (one for each of the p parameters). The only things
unknown in these systems of equations are the (that is, the vector
). This leads to a linear system of the form
where
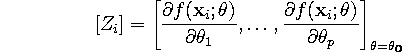
the row-vector of partials evaluated at the 
data location and using
the parameter estimates .
When we combine these systems for each of the n data locations, we end up with the linear system
where by 
we mean the model form evaluated at the
n data locations, with the current best parameter estimates
.
Our revised estimate for the parameters is thus given formally as
An alternative way to derive this same system of equations (again based on the linearization) is as follows: assuming that
we have that
which is better written in matrix form as
where Z is a constant matrix, and
.
This is just a linear regression problem, which we solve for 
:
and then our next estimate for is given by
Now iterate, as long as we're converging....