What is a Vertical Translation?

Vertically translating a graph is equivalent to shifting the base graph up or down in the direction of the y-axis. A graph is translated k units vertically by moving each point on the graph k units vertically.

The value of k determines the direction of the shift. Specifically,

Examples of Vertical Translations

Consider the following base functions,

(1) f (x) = 3x²,

(2) g(x) = 4x -1.

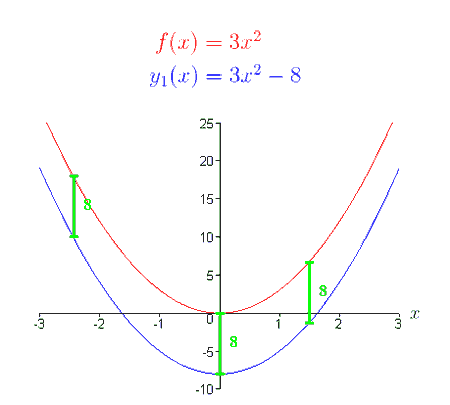
The graphical representation of function (1), f (x), is a parabola. What do you suppose the graph of

y₁ (x) = f (x) - 8

looks like? Using the definition of f (x), we can write y₁ (x) as,

y₁ (x) = f (x) - 8 = 3x² - 8.

Based on the definition of vertical shift, the graph of y₁ (x) should look like the graph of f (x), shifted down 8 units. Take a look at the graphs of f (x) and y₁ (x).

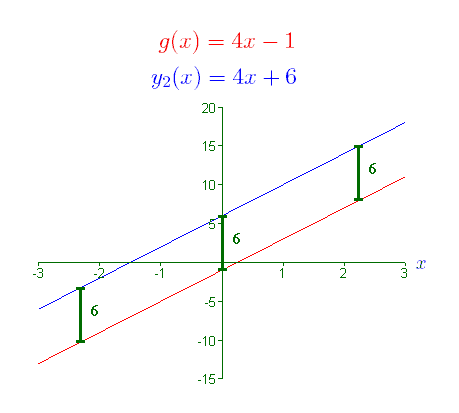
The graphical representation of function (2), g (x), is a line with a slope of 4 and a y -intercept at (0, -1). What would the graph of

y₂(x) = g (x) + 7

look like? Using our knowledge of vertical shifts, the graph of y₂(x) should look like the base graph g (x) sifted up 7 units. We can write y₂(x) as,

y₂(x) = g (x) + 7 = 4x -1 + 7 = 4x + 6

Therefore, the y-intercept has moved up 7 units, from (0,-1) for g(x) to (0,6) for y₂(x), as shown in the following graphs.

*****

In the next section, we will explore horizontal translations.

Horizontal Translations