BioMath: Quadratic Functions

The Biology Project > Biomath > Quadratic Function > Basics

Quadratic Functions

Basics

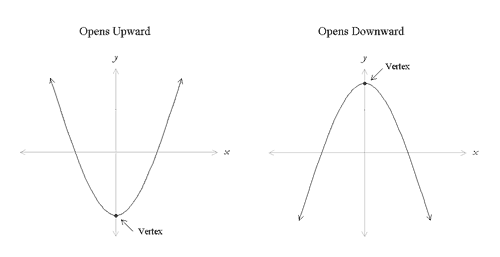
Definition and Symbolic Representation

Quadratic functions can be represented symbolically by the equation,

y(x) = ax² + bx + c,

where a, b, and c are constants, and a ≠ 0. This form is referred to as standard form. The coefficient a in this form is called the leading coefficient because it is associated with the highest power of x (i.e. the squared term).

Graphical Representation

Quadratic functions are nonlinear functions that are graphically represented by parabolas. Parabolas have a characteristic ∪-shape and open either upward or downward as shown below,

graph

A few things to notice about these graphs:

The lowest point of a parabola that opens upward is called the vertex of the parabola. The term vertex also refers to the highest point of a parabola that opens downward.

Parabolas are symmetric about a vertical line passing through the vertex. Parabolas that open upward decrease to the left of the vertex, and increase to the right of the vertex. Parabolas that open downward increase to the left of the vertex, and decrease to the right of the vertex.
Although the vertex is at the origin in each of these graphs, it is important to realize that the vertex of a parabola does not need to be located at the origin, nor does it need to lie on one of the axes.

Standard form provides clues to what the graph of a quadratic function will look like.

By inspecting a quadratic equation in standard form,

y(x) = ax² + bx + c,

you can get an idea of what the graph will look like. The leading coefficient tells you the direction the parabola opens, specifically

if a > 0, the parabola opens upward

if a < 0, the parabola opens downward.

In addition, the constant c is the y-intercept of the quadratic function. This fact can be derived mathematically by setting x = 0 (remember, points lying on the y-axis must have x-coordinate equal to zero) in the standard form of a quadratic equation yielding,

y(0) = a · 0² + b · 0 + c

y(0) = c.

Note that a quadratic function will always intersect the y-axis, but may not intersect the x-axis (we will discuss this topic in more detail later).

Finally, by inspecting the standard form of a quadratic equation, you can see that the domain of quadratic functions is all real numbers (i.e. there is no value of x that cannot be substituted into the equation y(x) = ax² + bx + c). The range of quadratic functions, however, is not all real numbers, but rather varies according to the shape of the curve. Specifically,

For a quadratic function that opens upward, the range consists of all y greater than or equal to the y-coordinate of the vertex.
For a quadratic function that opens downward, the range consists of all y less than or equal to the y-coordinate of the vertex.

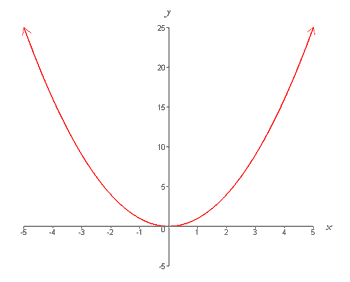
An example

The simplest quadratic function is given by y = x². To graph this function by hand, you can use a table of values as follows,

Table of values for y=x^2

By inspecting this table of values, you can see that the functional values are symmetric about the vertical line x = 0. You can plot these points in the xy-plane, and draw a smooth curve through them to form a parabola as below,

graph

*****

In the next section we explore how to find the vertex of a parabola.

Vertex of a quadratic function

The Biology Project > Biomath > Quadratic Functions > Basics

The Biology Project
Department of Biochemistry and Molecular Biophysics
The University of Arizona
January 2006
Contact the Development Team