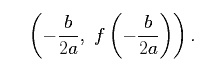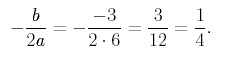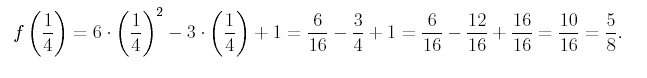Many applications of quadratic functions involve maximizing or minimizing a particular quantity. This can be easily done by determining the vertex of a parabola. If the parabola opens upward, the vertex represents the minimum of the function; while, if it opens downward, the vertex represents the maximum of the function.

To facilitate finding the vertex, it is often convenient to convert a quadratic equation from standard form , y(x) = ax² + bx + c, to vertex form,

y(x) = a(x − h)² + k,

where a ≠ 0.

By inspecting an equation in vertex form, you can determine:

For example, the quadratic equation

y = 4(x + 3)² − 9

has vertex (−3,−9) and opens upward.

If a quadratic function is given in standard form instead of vertex form, we can still find the vertex of the graph of that function. Specifically, the vertex of the graph of f(x) = ax² + bx + c is,

For example, consider the equation,

f(x) = 6x² - 3x +1,

noting that a = 6, b = -3, and c = 1. The x-coordinate of the vertex of the graph of f (x) is found as,

To find the y-coordinate of the vertex, we substitute x = 1/4 into f (x) as,

Therefore, we determine that the vertex of the graph is (1/4, 5/8).

*****

In the next section we will learn how to transform quadratic equations in standard form to vertex form by completing the square.

Completing the square