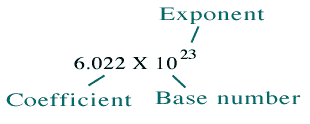The Biology Project > Biomath> Notation > Scientific Notation
Mathematical Notation
Scientific Notation
The speed of light is approximately 300,000,000 meters per second. Working with a large number such as this can quickly become awkward and cumbersome. To simplify matters, we often use scientific notation to represent very large and very small numbers.
Using scientific notation,300,000,000 m/sec can also be written as
3 x 100,000,000
or in the shorter form,
3 x 108,
where 8, the exponent, is the number of zeros.
As you see, the larger or the smaller the number the more beneficial the use of the scientific notation.
Positive exponents
Large numbers can be written in scientific notation by moving the decimal point to the left. For example, Avogadro's number is approximately 602,200,000,000,000,000,000,000 (where the decimal point implicitly resides to the right of the last zero). Using scientific notation this impressive number is simplified to: 6.022 x 1023
The decimal point is moved left to just after the first number. That first number must be at least 1, but less than 10. In the example above, the decimal point has been moved 23 places to the left. That number is now the positive exponent of the base 10.
Negative exponents
Numbers less than 1 can be expressed in scientific notation by moving the decimal point to the right. For example, how would we express 0.0006022?
We still have to follow the convention of scientific notation that the first number must be a least 1, but less than 10. In this instance, the decimal point needs to move to the right by 4 places to the first non-zero number. For every place we move the decimal to the right we decrease the power of ten by one, starting from zero. That number can be written as 6.022 x 10-4 .
*****
In the next section we will introduce set-builder and interval notations.
Set-Builder and Interval Notations
The Biology Project > Biomath> Notation > Scientific Notation
Department of Biochemistry and Molecular Biophysics
The University of Arizona
January 2006
Contact the Development Team
http://www.biology.arizona.edu All contents copyright © 2006. All rights reserved.