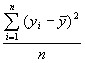 is multiplied by
is multiplied by 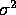 . Moreover, the variance of the sampling distribution of s2 is deflated by replacing the population mean,
. Moreover, the variance of the sampling distribution of s2 is deflated by replacing the population mean,
UNDERSTANDING SPATIAL ASSOCIATIONS
Outline
The outline of the module is as follows:
The Module
I. Readings
This module assumes that you have read the appropriate sections of
Haining, R., 1990, Spatial Data Analysis in the Social and Environmental Sciences, CPU, pp. 161-166 & 313-323
Haining, R., 1991, "Bivariate correlation with spatial data," Geographical Analysis, 23: 210-227 (especially pp. 216-224).
Richardson, S., 1990, "A method for testing the significance of geographical correlations with application to industrial lung cancer in France," Statistics in Medicine, 9: 515-528 (especially pp. 522-526).
What do we learn from these readings? They reveal some of the consequences of ignoring spatial correlation when estimating and interpreting means and bivariate correlation coefficients. This lecture furnishes some very useful approximation simplifications that allow you to avoid having to deal with matrix operations, if you wish.
II. Motivation
Two principal questions arise when dealing with georeferenced data containing spatial autocorrelation:
This first question can be addressed by focusing on one of the various meanings of spatial autocorrelation. This second question can be addressed by studying spatial statistical results.
Consider a conventional statistics context, where two variables, say X and Y, whose measurements were collected for iid (i.e., independent and identically distributed) observations and are correlated. In terms of regression, the square of the correlation coefficient indicates the percent of variance held in common by these two variables—the amount of the variation in one variable accounted for by the variation exhibited by the other variable. In other words, the squared correlation coefficient indexes the amount of redundant information contained in X and Y. If the correlation coefficient is 1 or -1, then all of the information contained in X also is contained in Y—once X is measured, then nothing additional is gained by measuring Y, and vice versa. If the correlation is 0.7, then roughly 50% of the information is held in common—once X is measured, then each measurement made for Y adds only about half an increment of new information, and vice versa. Spatial autocorrelation can be viewed in the same light, but in terms of attribute measures at locations (i.e., observations) for a single georeferenced variable. If the autocorrelation is 1, then once a measurement is taken at one location, it is known at all locations. In other words, obtaining additional measurements at other locations fails to furnish any new information. If the autocorrelation is 0.7, then the first measurement taken furnishes 100% completely new information. But each subsequent measurement taken at a nearby location will furnish only a fraction of new information. The only way to obtain 100% completely new information is to take measurements at locations that are sufficiently far apart that the autocorrelation amongst them essentially is zero. This rarely happens in practice, especially for epidemiological cases that have been aggregated according to their respective locations within administrative districts. Because each geographic observation contains partially unique information (i.e., spatial autocorrelation never is 1, and as a rule of thumb often falls in the range 0.4 to 0.6), and because data cannot--and in many situations should not--be discarded when they contain spatial autocorrelation, researchers need to employ statistical techniques that properly account for this autocorrelation.
Much of conventional statistical theory was developed using the iid assumption. This theory is replete with formulae including sample size (n) and degrees of freedom (df) terms. Accounting for the redundant information contained in georeferenced data can involve calculating the equivalent sample size and/or degrees of freedom for an iid data set. These equivalencies may be defined as effective sample size (n*) and effective degrees of freedom(df*); respectively they equal n and df when spatial autocorrelation is zero, and n* equals 1 when spatial autocorrelation is 1.
Two statistical tests commonly employed by epidemiologists that can be
modified to properly account for the presence of spatial autocorrelation in
georeferenced data are the t-test performed on single sample means, and the
t-test performed on bivariate correlation coefficients. Complications
emerging in these two problems that lie dormant with iid data
include: variance inflation/deflation factors (VIF/VDF), effective sample
size differing from n, and autocorrelation estimation (denoted by ![]() ). The notion of VIF
frequently is encountered when studying linear regression. But it also is
encountered, albeit not labeled as such, in elementary statistics contexts
such as the sampling distribution of the sample variance. In this instance,
the mean squared deviation formula
). The notion of VIF
frequently is encountered when studying linear regression. But it also is
encountered, albeit not labeled as such, in elementary statistics contexts
such as the sampling distribution of the sample variance. In this instance,
the mean squared deviation formula 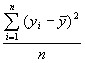 is multiplied by
is multiplied by ![]() in order to have E(s2) =
in order to have E(s2) = 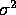 . Moreover, the variance of the sampling distribution of s2 is deflated by replacing the population mean,
. Moreover, the variance of the sampling distribution of s2 is deflated by replacing the population mean,
![]() ,
with its sample statistic counterpart,
,
with its sample statistic counterpart, ![]() ; this variance deflation is compensated for by multiplying s2 by the inverse of the VDF =
; this variance deflation is compensated for by multiplying s2 by the inverse of the VDF = ![]() in order to inflate the variance to its proper level.
in order to inflate the variance to its proper level.
The notion of effective sample size, albeit again not labeled as such, also is encountered in the elementary statistics context of a difference of two means when the variances are unequal. Here the effective sample size initially was estimated by Satterthwaite as
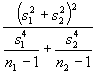 + 2,
+ 2,
where sj and nj respectively denote the standard deviation and sample size for subsample j. This formula can render fractional values for n*, a noteworthy property since fractional effective sample sizes are common in spatial statistics.
A number of spatial autoregressive model specifications are used in practice. One popular specification is the simultaneous autoregressive (SAR) model, based upon a row-standardized geographic weights matrix. This specification casts each locationally tagged attributed value, yi, as a function of the weighted average of its nearby, surrounding attribute values, namely
This specification also conceptualizes spatial autocorrelation as being contained in the regression model error term. And, theoretically this specification relates to the Bessel function semivariogram model in geostatistics. The equational form of the SAR model is, using matrix notation (denoted by bold letters),
where Y is an n-by-1 vector for the dependent variable (i.e., the regressand), Z is an n-by-(p+1) matrix of predictor variables (i.e., the regressors), ß is a (p+1)-by-1 vector of regression parameters,
![]() is an n-by-1 vector of iid N(0,
is an n-by-1 vector of iid N(0, ![]() ) error terms, I is an n-by-n identity matrix, W is an n-by-n row-standardized geographic weights matrix—often converted from a binary, 0-1 contiguity matrix based upon “rook's” adjacencies (drawing an analogy with chess moves)—and
) error terms, I is an n-by-n identity matrix, W is an n-by-n row-standardized geographic weights matrix—often converted from a binary, 0-1 contiguity matrix based upon “rook's” adjacencies (drawing an analogy with chess moves)—and
![]() is the spatial autoregressive parameter for variable Y. In general,
though, let the spatial covariance matrix be denoted by
is the spatial autoregressive parameter for variable Y. In general,
though, let the spatial covariance matrix be denoted by
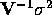 ,
which for this SAR model yields
,
which for this SAR model yields
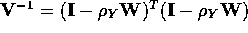 ,
where T denotes the matrix operation of transpose. Of note is that the spatially filtered version of variable Y, say Y*, is given by the matrix product
,
where T denotes the matrix operation of transpose. Of note is that the spatially filtered version of variable Y, say Y*, is given by the matrix product
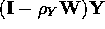 .
.
Case 1: the sample mean ![]() (the univariate case)
(the univariate case)
Consider the sampling distribution of the mean, ![]() . For iid data, the variance of this sampling distribution is given by
. For iid data, the variance of this sampling distribution is given by ![]() . In contrast, for georeferenced data this variance is given by
. In contrast, for georeferenced data this variance is given by ![]() . Of note is that for iid data, V-1 = I and this latter expression reduces to
. Of note is that for iid data, V-1 = I and this latter expression reduces to ![]() , whereas if spatial autocorrelation equals 1, conceptually speaking this latter expression reduces to
, whereas if spatial autocorrelation equals 1, conceptually speaking this latter expression reduces to ![]() . Meanwhile, positive spatial autocorrelation causes an inflation of the variance. The accompanying VIF is given by
. Meanwhile, positive spatial autocorrelation causes an inflation of the variance. The accompanying VIF is given by ![]() , where TR denotes the matrix trace operator. The extent of this inflation is illustrated in Figure 1, which was constructed from results of a simulation experiment. Combining this result with the conventional adjustment for variance, and taking into account the estimation of
, where TR denotes the matrix trace operator. The extent of this inflation is illustrated in Figure 1, which was constructed from results of a simulation experiment. Combining this result with the conventional adjustment for variance, and taking into account the estimation of
![]() , renders
, renders 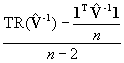 as the VIF estimator.
as the VIF estimator.
Determining the effective sample size for this univariate case requires the following algebraic manipulations:
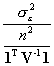 =
= 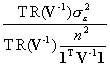 =
= 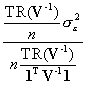 .
.
Hence the effective sample size is given by n* = ![]() . Of note is that if spatial autocorrelation is zero, this expression reduces to n; if spatial autocorrelation is 1, conceptually this expression reduces to 1.
. Of note is that if spatial autocorrelation is zero, this expression reduces to n; if spatial autocorrelation is 1, conceptually this expression reduces to 1.
Consequently, when computing the t-statistic for the mean of a georeferenced variable, where the spatial autoregressive parameter
![]() has been estimated, the effective degrees of freedom used should be
has been estimated, the effective degrees of freedom used should be
Case 2: the correlation coefficient r (the bivariate case)
Consider the sampling distribution of the bivariate correlation coefficient, r. For iid sample data, the variance of this sampling distribution is given by ![]() . In contrast, for georeferenced data this variance may be approximated with a simulation experiment. This experiment would begin by generating two n-by-1 vectors of iid N(0,1) pseudo-random variables, one for variable X and one for variable Y; respectively denote these pseudo-random variables by, say,
. In contrast, for georeferenced data this variance may be approximated with a simulation experiment. This experiment would begin by generating two n-by-1 vectors of iid N(0,1) pseudo-random variables, one for variable X and one for variable Y; respectively denote these pseudo-random variables by, say,
![]() and
and
![]() .
Next, both X and Y would have spatial autocorrelation embedded as follows:
.
Next, both X and Y would have spatial autocorrelation embedded as follows:
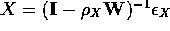 and
and
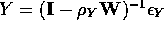 ,
,
where
III. Decision-making in the presence of spatial autocorrelation: spatial statistical theory simulation and matrix results
Two decision-making problems are explored here. The first asks what the average incidence of a geographically distributed disease is in the population. The second asks whether or not a relationship exists between two georeferenced disease incidences in the population.
The statistical theory is based upon an assumption of normality. This assumption may be satisfied through the central limit theorem when the sample mean, ![]() , is being analyzed. But the central limit theorem holds only when the sample size is sufficiently large, somewhere between 30 and 100 depending upon the underlying frequency distribution for the variable Y. Unfortunately, the effective sample size tends to be substantially less than n when even modest levels of spatial autocorrelation are latent in a georeferenced variable. Meanwhile, often derivations for the sampling distribution of the correlation coefficient, r, assume bivariate normality. Serendipitously, this tends to be the situation linking directly to linear relationships. When empirical data for either of these cases fails to exhibit the necessary normality, Box-Cox power transformations often are employed.
, is being analyzed. But the central limit theorem holds only when the sample size is sufficiently large, somewhere between 30 and 100 depending upon the underlying frequency distribution for the variable Y. Unfortunately, the effective sample size tends to be substantially less than n when even modest levels of spatial autocorrelation are latent in a georeferenced variable. Meanwhile, often derivations for the sampling distribution of the correlation coefficient, r, assume bivariate normality. Serendipitously, this tends to be the situation linking directly to linear relationships. When empirical data for either of these cases fails to exhibit the necessary normality, Box-Cox power transformations often are employed.
The Box-Cox power transformation approach adopted here seeks a translation (![]() )
and a stretching/shrinking exponent parameter (
)
and a stretching/shrinking exponent parameter (![]() )
for a georeferenced variable Y whose Shapiro-Wilk statistic is significantly
less than 1 in order to most closely align the transformed values with those
for a theoretical quantile plot. In other words, a function is
sought such that the transformed values most closely align with their
corresponding approximate theoretical values given by the normal curve
z-score values for the percentiles
)
for a georeferenced variable Y whose Shapiro-Wilk statistic is significantly
less than 1 in order to most closely align the transformed values with those
for a theoretical quantile plot. In other words, a function is
sought such that the transformed values most closely align with their
corresponding approximate theoretical values given by the normal curve
z-score values for the percentiles
(ri - 3/8)/(n + 1/4) , i = 1, 2,..., n,
where ri denotes the rank of the Y attribute value for location i. This function frequently may be identified with a nonlinear regression routine that regresses the quantile values on one of the following two functional forms:
![]() , for
, for ![]() = 0,
= 0,
where J1 =
![]() ÿ
ÿ![]() -1 (ÿ denotes the geometric mean of the data) and J2 = ÿ. Of note is that there is no guarantee that either of these functions will render a successful transformation.
-1 (ÿ denotes the geometric mean of the data) and J2 = ÿ. Of note is that there is no guarantee that either of these functions will render a successful transformation.
The impact of a power transformation is illustrated in Figures 2a and 2b. The quantile plot for a "social class" measure, used to quantify one type of exposure risk in Glasgow, appears in Figure 2a. The left-hand hook exhibited in this plot is characteristic of a log-normal distribution. The corresponding power-transformed plot for this measure—based upon LN(X + 0.01)—appears in Figure 2b. Not only has the hook disappeared, but this second quantile plot exhibits a much closer alignment of the data with the theoretical linear normal distribution line.
A researcher needs to keep in mind that the inferential basis for the Shapiro-Wilk statistic can be corrupted by the presence of spatial autocorrelation. Hence, its calculation for spatially filtered data values can be quite informative.
Case 1: confidence intervals for the sample mean ![]()
The first simulation experiment utilizes the Glasgow geographic landscape. Consider the "all deaths" georeferenced disease incidence variable. This attribute variable has the following statistical descriptors:
![]() = 0.70108,
= 0.70108, ![]() = 100.951,
= 100.951, ![]() = 17.476, spatially filtered MC = 0.05278 (GR = 0.91334), Shapiro-Wilk =0.97771 (prob = 0.46),
= 17.476, spatially filtered MC = 0.05278 (GR = 0.91334), Shapiro-Wilk =0.97771 (prob = 0.46), ![]() = 104.035 ,
= 104.035 ,
where ![]() =
= ![]() ; of note is that if
; of note is that if
![]() = 0 then
= 0 then ![]() =
= ![]() . This Shapiro-Wilk statistic implies that the frequency distribution of "all deaths" aggregated by administrative district does not differ from a normal frequency distribution in the population. Converting variable Y to z-scores, for simplicity, and computing the spatially filtered z-score counterparts yields the following statistical descriptors:
. This Shapiro-Wilk statistic implies that the frequency distribution of "all deaths" aggregated by administrative district does not differ from a normal frequency distribution in the population. Converting variable Y to z-scores, for simplicity, and computing the spatially filtered z-score counterparts yields the following statistical descriptors:
![]() * = 0.05191, VIF = 1.65020, se = 0.76851, Shapiro-Wilk = 0.96559 (prob = 0.09) .
* = 0.05191, VIF = 1.65020, se = 0.76851, Shapiro-Wilk = 0.96559 (prob = 0.09) .
Clearly the spatially filtered data conform to a normal frequency distribution in the population.
A simulation experiment utilizing these data features was conducted that involved 5,000 replications. Eighty-seven pseudo-random numbers were drawn from a normal distribution having
![]() = 0.05191 (from
= 0.05191 (from ![]() *) and
*) and
![]() = 0.76851 (from se). The simulation results rendered
= 0.76851 (from se). The simulation results rendered
![]() = 0.05106,
= 0.05106, ![]() = 0.08169 (versus
= 0.08169 (versus ![]() = 0.08229),
= 0.08229), ![]() = 0.76686 .
= 0.76686 .
These simulation results compare very favorably with their empirical/theoretical counterparts.
The next step in the simulation exercise was to embed spatial autocorrelation into each pseudo-random numbers vector, prespecifying ![]() = 0.70108, using
= 0.70108, using
Y = 17.476
[(I – 0.70108W)-1
![]() + 100.951] .
+ 100.951] .
After this step the simulation results rendered
![]() = 104.00,
= 104.00, ![]() = 4.987 (versus
= 4.987 (versus 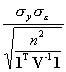 = 5.03),
= 5.03), ![]() = 17.201 .
= 17.201 .
Again these results compare very favorably with their empirical/theoretical counterparts, but with ![]() relating directly to
relating directly to ![]() rather than
rather than ![]() .
.
One important demonstration here is that the sampling error for the mean is 5.03 rather than ![]() = 1.87. The degrees of freedom for the t statistic also are altered: df = 87 – 1 (t86,0.975 = 1.9879) needs to be replaced with df* = 12.9 – 2 (t10.9,0.975 = 2.2035). Therefore, the resulting 95% confidence interval for the mean incidence of "all deaths" is (92.96, 115.12) rather than (97.22, 104.68), a marked difference. In other words, the conventional inferential basis for decision-making is substantially corrupted by the latent moderate level of spatial autocorrelation present in these georeferenced disease incidence values. For the most part, this corruption impacts upon precision.
= 1.87. The degrees of freedom for the t statistic also are altered: df = 87 – 1 (t86,0.975 = 1.9879) needs to be replaced with df* = 12.9 – 2 (t10.9,0.975 = 2.2035). Therefore, the resulting 95% confidence interval for the mean incidence of "all deaths" is (92.96, 115.12) rather than (97.22, 104.68), a marked difference. In other words, the conventional inferential basis for decision-making is substantially corrupted by the latent moderate level of spatial autocorrelation present in these georeferenced disease incidence values. For the most part, this corruption impacts upon precision.
Case 2: significance of the correlation coefficient r
The covariation for two georeferenced variables also has a variance inflation factor associated with it. In its simplest form, this VIF is given by![]() ; in its sample statistics form, this VIF is given by
; in its sample statistics form, this VIF is given by ![]() -
- ![]() , for which both the two means and the two spatial autoregressive parameters have been estimated. But when this VIF is divided by the VIFs for the variances of X and Y, it becomes a variance deflation faction. In its simplest form, for example, it becomes
, for which both the two means and the two spatial autoregressive parameters have been estimated. But when this VIF is divided by the VIFs for the variances of X and Y, it becomes a variance deflation faction. In its simplest form, for example, it becomes 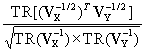 . In other words, the covariation inflation for two georeferenced variables tends to be more than compensated for by the product of the individual variance inflations, yielding a variance deflation factor (VDF), which is sensible since a correlation coefficient cannot exceed 1. In practice this VDF tends to be close to 1.
. In other words, the covariation inflation for two georeferenced variables tends to be more than compensated for by the product of the individual variance inflations, yielding a variance deflation factor (VDF), which is sensible since a correlation coefficient cannot exceed 1. In practice this VDF tends to be close to 1.
As often is the case, the major impact of spatial autocorrelation with regard to a correlation coefficient is on the variance of its sampling distribution. Suppose the variance of the sampling distribution of r is given by ![]() . Then given that
. Then given that ![]() , the effective sample size, say
, the effective sample size, say ![]() , may be defined as
, may be defined as ![]() =
= ![]() =
= ![]() This effective sample size can be approximated by simulating the sampling distribution, such that
This effective sample size can be approximated by simulating the sampling distribution, such that ![]() =
= ![]() . The steps of the necessary simulation experiment used to calculate
. The steps of the necessary simulation experiment used to calculate ![]() are outlined earlier in this discussion (see Case 2 of Section II).
are outlined earlier in this discussion (see Case 2 of Section II).
Again using the Glasgow geographic landscape, consider the "cancer mortality rates" variable together with the "percentage of households living in poor accommodation lacking basic amenities" (a "social class" surrogate). Let this first variable be Y and this second variable be X. This first variable can be transformed in order to obtain an acceptable Shapiro-Wilk statistic using LN(Y – 23). Unfortunately, a power transformation does not exist for variable X that yields an acceptable Shapiro-Wilk statistic. As an aside, Haining (1991, p. 216) suggests three possible transformations, all of which can be improved upon:
X0.3 – (X + 0.7)0.3 is superior to Haining's suggested X1/2 + (X + 1)1/2 ,
LN(X + 0.01) is superior to Haining's suggested LN(X + 1) , and
(X + 0.02)-0.1 is superior to Haining's suggested (X + 1)-1 .
For purposes of analysis, the logarithmic transformation has been employed here--which is the same type of transformation selected by Haining. A plot of these relationships appears in Figure 3, with o's (o) denoting results produced by Haining's power transformation and pluses (+) denoting results produced by the power transformation used here.
First, the correlation coefficient between the two selected transformed georeferenced variables is 0. 206, which is slightly less than the r = 0.245 value reported by Haining for Y with LN(X + 1). The VDF here is 0.99722, which essentially is 1. A simulation experiment for this case--for which
![]() = 0.70581 and
= 0.70581 and
![]() = 0.63716, and involving 5,000 replications--yields
= 0.63716, and involving 5,000 replications--yields ![]() = 0.15391 for the autocorrelated data and 0.10814 for the unautocorrelated data. This second value compares very favorably with its theoretical counterpart of 0.10847. Hence,
= 0.15391 for the autocorrelated data and 0.10814 for the unautocorrelated data. This second value compares very favorably with its theoretical counterpart of 0.10847. Hence, ![]() =
= ![]() = 44.2.
= 44.2.
Now the corresponding significance tests here may be written as follows, with regard to spatial autocorrelation acknowledgement:
ignoring: ![]() = 1.89914 < t85,0.975 = 1.9883 ,
= 1.89914 < t85,0.975 = 1.9883 ,
accounting for: ![]() = 1.33844 << t42.2,0.975 = 2.0178 .
= 1.33844 << t42.2,0.975 = 2.0178 .
Using Haining's value for r of 0.245 yields the respective test statistics of 2.25869 and 1.59184. Therefore, taking spatial autocorrelation into account strongly implies that there is no relationship between Glasgow "cancer mortality rates" and "percentage of households living in poor accommodation lacking basic amenities" in the population.
An alternative testing procedure is to compute the correlation between the residuals from SAR model fits, namely the vectors eX and eY—the estimates of
![]() and
and
![]() .
These values are the results of filtering spatial autocorrelation from variables X and Y. The correlation coefficient based upon these filtered vectors relates more directly to classical statistical theory. But because
.
These values are the results of filtering spatial autocorrelation from variables X and Y. The correlation coefficient based upon these filtered vectors relates more directly to classical statistical theory. But because ![]() and
and ![]() also are calculated with the sample data, a conservative estimate of the standard error of r is given by
also are calculated with the sample data, a conservative estimate of the standard error of r is given by ![]() . Returning to the Glasgow example, then,
. Returning to the Glasgow example, then, ![]() = 0.064, where the respective MCs for these residuals are 0.03129 and –0.02246. The accompanying t statistic is
= 0.064, where the respective MCs for these residuals are 0.03129 and –0.02246. The accompanying t statistic is ![]() = 0.58307 << t83,0.975 = 1.9890. This result confirms the previous finding based upon taking spatial autocorrelation into account, namely that the relationship between X and Y is not significant. Drawbacks affiliated with this approach include: (1) a researcher is working with a metric even further removed from the original measurement scale for a georeferenced variable, and (2) each set of residuals is not independent in a traditional sense, with impacts of this dependency not well understood.
= 0.58307 << t83,0.975 = 1.9890. This result confirms the previous finding based upon taking spatial autocorrelation into account, namely that the relationship between X and Y is not significant. Drawbacks affiliated with this approach include: (1) a researcher is working with a metric even further removed from the original measurement scale for a georeferenced variable, and (2) each set of residuals is not independent in a traditional sense, with impacts of this dependency not well understood.
IV. Graphical depictions
As can be seen from the discussion thus far, calculations pertaining to measuring the nature and degree of spatial autocorrelation (![]() and
and ![]() ), effective sample size (n* and
), effective sample size (n* and ![]() ), and effective degrees of freedom (df*) require lots of matrix algebra. Fortunately these quantities display strong patterns across both simulation results and empirical case studies.
), and effective degrees of freedom (df*) require lots of matrix algebra. Fortunately these quantities display strong patterns across both simulation results and empirical case studies.
The MC is relatively simple to calculate, even for massively large georeferenced data sets. The SAR spatial autocorrelation parameter requires calculating the eigenvalues of a geographic contiguity matrix as well as nonlinear regression involving iterative nonlinear optimization. But the covariation between MC and ![]() for the SAR model displays a strong and reasonably precise linear relationship, which is portrayed in Figure 4; the observed relationship is denoted by o's (o), whereas the predicted values are denoted by pluses (+). This graph was constructed from empirical data results associated with acceptable Shapiro-Wilk statistics, including those for the Glasgow data.
for the SAR model displays a strong and reasonably precise linear relationship, which is portrayed in Figure 4; the observed relationship is denoted by o's (o), whereas the predicted values are denoted by pluses (+). This graph was constructed from empirical data results associated with acceptable Shapiro-Wilk statistics, including those for the Glasgow data.
Calculating the effective sample size for a univariate georeferenced data analysis involves matrix inversion. But the relationship between this quantity and the SAR spatial autocorrelation parameter exhibits a very strong and very precise nonlinear trend, which is portrayed in Figure 5. This graph was constructed from both empirical data results and simulation experiment results; in Figure 5 the empirical relationship is denoted by o's (o), the simulation relationship is denoted by dots (.), and the predicted values are denoted by pluses (+). The simulation results follow a smooth curve, whereas the empirical data results slightly scatter about this smooth curve.
Calculating the effective sample size for a bivariate georeferenced data analysis involves matrix inversion coupled with extensive simulation work. The relationship between this measure and each of the SAR spatial autocorrelation parameters exhibits a very strong and very precise nonlinear trend, which is portrayed in Figure 6. This graph was constructed from a series of simulation experiments employing the geographic weights matrix for the Glasgow geographic landscape; the simulated relationship with regard to
![]() is denoted by o's (o), whereas the simulated relationship with regard to
is denoted by o's (o), whereas the simulated relationship with regard to
![]() is denoted by pluses (+). The simulation results follow the same scatterplot for variables X and Y, which is sensible. The horizontal alignment of points in the upper right-hand quadrant of the graph are for cases where only one of the autocorrelation parameters equals 0; the cluster of points on the right-hand part of the graph are for cases where
is denoted by pluses (+). The simulation results follow the same scatterplot for variables X and Y, which is sensible. The horizontal alignment of points in the upper right-hand quadrant of the graph are for cases where only one of the autocorrelation parameters equals 0; the cluster of points on the right-hand part of the graph are for cases where
![]()
![]()
![]() .
Of note is that the range of negative spatial autocorrelation is governed by the smallest eigenvalue of the geographic weights matrix (i.e.,
.
Of note is that the range of negative spatial autocorrelation is governed by the smallest eigenvalue of the geographic weights matrix (i.e., ![]() = -1.57228 for the Glasgow surface partitioning).
= -1.57228 for the Glasgow surface partitioning).
The most useful feature captured by these graphs is that the relationships of interest are conspicuous and well-behaved. This behavior allows these graphs to be succinctly described with equations.
V. Some useful equations
The graphs appearing in Figures 4-6 reveal rather smooth curves depicting relationships. Fitting equations to these curves yields useful equations for approximating the quantities of interest, namely the SAR autocorrelation parameter, ![]() , and the effective sample sizes, n* and nXY*.
, and the effective sample sizes, n* and nXY*.
Figure 4 implies the following equation:
![]() =
= 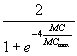 -
- 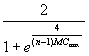 ,
,
where MCmax denotes the maximum positive MC value that can be calculated with a given surface partitioning. This extreme MC value roughly equals ![]() , where
, where
![]() is the second eigenvalue of the geographic weights matrix C used to calculate MC. This equation was specified in such a way that
is the second eigenvalue of the geographic weights matrix C used to calculate MC. This equation was specified in such a way that ![]() is identically
0 when MC =
is identically
0 when MC = ![]() . For the empirical cases used to construct Figure 4, pseudo-R2 = 0.878. The predicted values align reasonably well with their empirical counterparts. A 15-by-15 lattice simulation experiment—for which MCmax = 1.05084--further confirmed this equational form, yielding pseudo-R2 = 0.999. The graph for this result appears in Figure 7; the simulated relationship is denoted by o's (o), whereas the predicted values are denoted by pluses (+).
. For the empirical cases used to construct Figure 4, pseudo-R2 = 0.878. The predicted values align reasonably well with their empirical counterparts. A 15-by-15 lattice simulation experiment—for which MCmax = 1.05084--further confirmed this equational form, yielding pseudo-R2 = 0.999. The graph for this result appears in Figure 7; the simulated relationship is denoted by o's (o), whereas the predicted values are denoted by pluses (+).
Meanwhile, Figure 5 implies the following equation:
![]() = n
[1 – 2.67978
= n
[1 – 2.67978![]() (1 -
(1 -![]() )] .
)] .
For the empirical cases used to construct Figure 5, the pseudo-R2 = 0.998. The specification of this equation has been formulated in order to insure that when ![]() = 0 then
= 0 then ![]() = n, and when
= n, and when ![]() = 1 then
= 1 then ![]() = 1.
= 1.
Finally, Figure 6 implies the following equation:
![]() = n
= n
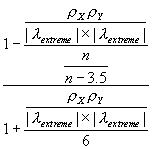 - 2 = 1 + (n-3)
- 2 = 1 + (n-3)
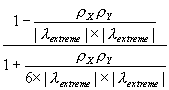 ,
,
where the extreme eigenvalues are
![]() for positive spatial autocorrelation and
for positive spatial autocorrelation and
![]() for negative spatial autocorrelation, and are extracted from the row-standardized geographic weights matrix W. Because matrix W is row-standardized,
for negative spatial autocorrelation, and are extracted from the row-standardized geographic weights matrix W. Because matrix W is row-standardized, ![]() is theoretically known to always equal 1; hence for the very common case of both X and Y containing positive spatial autocorrelation, the equation reduces to
is theoretically known to always equal 1; hence for the very common case of both X and Y containing positive spatial autocorrelation, the equation reduces to ![]() = 1 + (n-3)
= 1 + (n-3)
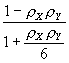 . This equation is similar to that known for time series (see Haining, 1991, p. 314), and that reported by Richardson and Hemon, 1982). Two noteworthy differences are the appearance of
. This equation is similar to that known for time series (see Haining, 1991, p. 314), and that reported by Richardson and Hemon, 1982). Two noteworthy differences are the appearance of ![]() in the case of negative spatial autocorrelation, and the appearance of 6 in the denominator. This value of 6 may be specific to the Glasgow medical districts surface partitioning. For the simulation experiments used to construct Figure 6 also were used to evaluate the equation for
in the case of negative spatial autocorrelation, and the appearance of 6 in the denominator. This value of 6 may be specific to the Glasgow medical districts surface partitioning. For the simulation experiments used to construct Figure 6 also were used to evaluate the equation for ![]() ; the accompanying scatterplot appears in Figure 8, for which pseudo-R2 = 0.996.
; the accompanying scatterplot appears in Figure 8, for which pseudo-R2 = 0.996.
VI. Applications
Selected georeferenced variables for Glasgow have been used throughout this discussion for illustrative purposes. The remaining variables in Haining's data set are analyzed in this section. Confirming these results is a good exercise for the reader to pursue. Extending this category of spatial analysis to data, such as those reported by county by the New York State Department of Health (http://www.health.state.ny.us/nysdoh/cancer), also is a worthwhile exercise for the reader to pursue.
Standard mortality rates for both "all deaths" and "cerebro-vascular" appear to conform to a normal frequency distribution in the population; their respective Shapiro-Wilk statistics are 0.97771 (prob = 0.46) and 0.97296 (prob = 0.26). Three of the remaining standardized rates require a power transformation:
LN(accidents + 89): Shapiro-Wilk = 0.98615 (prob = 0.85)
LN(respiratory + 32): Shapiro-Wilk = 0.97398 (prob = 0.30)
LN(cancer – 23): Shapiro-Wilk = 0.97869 (prob = 0.50)
Meanwhile, the standardized mortality rate for "ischaemic heart disease" has one extremely high and one extremely low rate, with these two outliers causing deviation from normality. Once these two anomalies are accounted for, the frequency distribution conforms acceptably well to a bell-shaped curve [i.e., Shapiro-Wilk = 0.98178 (prob = 0.66)].
To simplify comparisons here, all variables have been converted to z-scores, resulting in ![]() = 1. For Glasgow, MCmax = 1.07829. Univariate analysis results are summarized in Table 1.
= 1. For Glasgow, MCmax = 1.07829. Univariate analysis results are summarized in Table 1.
|
Table 1: Univariate results for Haining's Glasgow data |
|||||||
|
variable |
|
MC |
|
VIF |
|
n* |
|
|
All deaths |
0.70108 |
0.42670 |
0.68079 |
1.65020 |
0.59889 |
12.9 |
13.2 |
|
Accidents |
0.51561 |
0.29308 |
0.51727 |
1.24176 |
0.79733 |
25.0 |
25.5 |
|
Respiratory |
0.54626 |
0.30537 |
0.53427 |
1.28423 |
0.76515 |
22.7 |
23.2 |
|
Cancer |
0.63716 |
0.39776 |
0.64935 |
1.45876 |
0.67531 |
16.6 |
17.0 |
|
Heart disease |
0.50405 |
0.23218 |
0.42742 |
1.22733 |
0.81576 |
25.9 |
26.4 |
|
Cerebro-vascular |
0.35573 |
0.17466 |
0.33465 |
1.09805 |
0.92260 |
39.1 |
39.7 |
|
Social class |
0.70581 |
0.46609 |
0.72013 |
1.66780 |
0.56334 |
12.6 |
13.0 |
Multiplying an error variance, ![]() , by its corresponding theoretical VIF results in a variance value for the associated georeferenced variable of approximately 1 (e.g., 0.59889*
1.65020 = 0.98829). Clearly, using the values for
, by its corresponding theoretical VIF results in a variance value for the associated georeferenced variable of approximately 1 (e.g., 0.59889*
1.65020 = 0.98829). Clearly, using the values for ![]() , which almost equal their
, which almost equal their ![]() counterparts, is far
better than using
counterparts, is far
better than using
![]() = 0. Similarly, using the values for
= 0. Similarly, using the values for ![]() , which also deviate little from their n* counterparts, is far better than using n = 87.
, which also deviate little from their n* counterparts, is far better than using n = 87.
Bivariate analysis results are summarized in Table 2.
|
Table 2: Bivariate results for Haining's Glasgow data |
|||||||
|
variable |
Correlation with social class |
VDF |
nXY* a la simulation |
|
t statistic |
|
t statistic |
|
All deaths |
0.354 |
0.99998 |
39.7 |
43.4 |
2.17296 |
0.191 |
1.74009 |
|
Accidents |
0.439 |
0.98361 |
51.5 |
53.3 |
3.08889 |
0.277 |
2.52359 |
|
Respiratory |
0.322 |
0.98774 |
59.3 |
52.2 |
2.21530 |
0.081 |
0.73795 |
|
Cancer |
0.206 |
0.99722 |
44.0 |
45.3 |
1.33437 |
0.064 |
0.58307 |
|
Heart disease |
0.309 |
0.98197 |
52.7 |
58.4 |
2.19958 |
0.251 |
2.28672 |
|
Cerebro-vascular |
0.178 |
0.95796 |
62.4 |
64.7 |
1.38314 |
0.116 |
1.05681 |
As expected, most of the VDF values are nearly 1. The ![]() values tend to be markedly less than their conventional counterparts. The
values tend to be markedly less than their conventional counterparts. The ![]() values furnish a reasonably good approximation to those nXY* values obtained with simulation experiments. For individual correlation coefficient tests the critical t statistics range from 1.9987 to 2.0216, indicating that four of the relationships are significant. The critical t statistic for the correlation coefficients calculated with filtered data is 1.9890, indicating that only two of the relationships are significant. These results suggest that a researcher should confidently expect relationships in the population only between social class and standardized mortality rates for accidents and for heart disease.
values furnish a reasonably good approximation to those nXY* values obtained with simulation experiments. For individual correlation coefficient tests the critical t statistics range from 1.9987 to 2.0216, indicating that four of the relationships are significant. The critical t statistic for the correlation coefficients calculated with filtered data is 1.9890, indicating that only two of the relationships are significant. These results suggest that a researcher should confidently expect relationships in the population only between social class and standardized mortality rates for accidents and for heart disease.
VII. Software