Variogram Modelling

For modelling I like Myers's 1991 paper ``On Variogram Estimation'' [3] for a general overview. (This paper considers much more than the estimation of variograms, including criteria for cross-validation.)

The usual estimator of the variogram function for lag (that is, for those pairs separted by a vector ) is

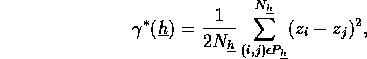
where is the number of distinct pairs of data values, placed in the set (pairs displaced by the vector ). I have shown in a previous lecture (lecture 3) that the sample variogram obtained using this estimator can be considered a spatial decomposition of the sample variance.

Variograms are modelled using the class of conditionally negative definite (CND) functions. It's not so important that you understand what that means, but you should know that it's not just any function which can serve as a variogram model. At present there is a ``zoo'' of functions which we use in the modelling functions, some of whose members we will look at below.

Any function which is CND can be used as a model: however, to ensure that the kriging system is invertible, it is essential that the CND function be strictly CND. The valid isotropic models (provided in the popular public-domain geostatistical software package Geo-EAS [1]) are

• the nugget model:

   

• the linear model:

   

• the power models (of which the linear is an example):

   

• the gaussian model:

   

• the spherical model:

   

• the exponential model:

   

(The factor of ln(20) in the gaussian and exponential models appears because the range r of those models is defined as the point at which the model attains 95% of its sill, c.) The linear model does not have a range, but increases linearly as .

The Guassian model and power models (for ) are the only model above that are ``concave up'' around zero (that is, shaped like a bowl that could hold water). The others are either flat (linear, nugget), or concave down at the origin.

Since conditionally negative definite functions form a positive cone in the space of functions (which is to say that positive linear combinations of such functions are again conditionally negative definite), one strategy for modelling variograms is to use positive combinations of known valid models to fit sample variograms. No one has yet developed, to our knowledge, a more general method.

Oftentimes, variograms are modelled using a weighted least-squares non-linear optimization, which is more complicated than it sounds, actually....