Andy Long
This summary of Ripley's K function is taken from Bailey and Gatrell[1].
The definition of the K function is as follows:
where 
is the intensity, or mean number of events per unit area.
If R is the area of region 
, then the expected number of events in
is 
.
Let 
be the distance between the 
and 
events
in , and 
be the indicator function which is 1 if 
and 0 otherwise. Then an estimate of K is given by
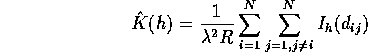
This estimate does not account for the fact that there may be pairs for which one partner point is outside the region, and hence unobservable. Thus an edge-corrected estimate of K is given by
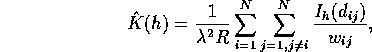
where 
is the conditional probability that an event is observed in
region , given that it is a distance from the event i.
(To understand how to calculate , draw a circle around the
point; if the circle intersects the boundary of , calculate the ratio
of the area inside the boundary to the whole area.)
The ordinary estimate of is N/R. Thus the computational
formula for 
becomes
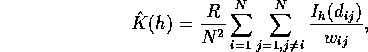
Note that we are always interested in values of h small compared to
the scale of region : ``it is not realistic to attempt to explore
second order effects which operate on the same physical scale as the dimensions
of [ ].''
As an exploratory tool, we need to consider what manner of comparison
we can make to help us interpret K. For a homogeneous Poisson process, the
number of events within a chosen distance h of an event would be just 
. This suggests a plot of
against a plot of f(h)=h.
``Under regularity K(h) would be less than , whereas under
clustering K(h) would be greater than .'' Hence, where L(h) is
above the identity function line, we imagine that there is clustering at that
scale; where it is below, there is greater regularity than we would expect in
the face of a Poisson process.