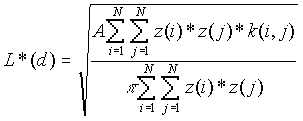 [1]
[1]Weighted K-Function
The weighted K-function was developed by Getis (1992) based on the K-function or second order analysis (see K-function). The statistical test is based on the permutations of weighted values at points. For the test, values at points are randomly assigned to the points repeatedly in order to create a confidence envelope.
Input
You’ll be asked to enter the input data file. This file should contain coordinates and the weight for each point (z). You will also be prompted to enter the maximum distance of study, the number of distance increments, and the number of permutations to use in creation of the confidence envelope.
Analysis
Before performing weighted K-function analysis, K-function analysis should be carried out to determine if the points show a clustered, dispersed, or a CSR pattern. Weighted K-function analysis is then used to determine if the rates or values at each point are clustered, dispersed, or random within the pattern of points. In some sense then, the pattern of weights is independent of location in the simulation. L*(d) includes the interaction of each point with itself, while L(d) does not. An observed L(d) below the minimum expected L(d) indicates that the values are dispersed, whereas an observed L(d) above the maximum expected L(d) indicates that clustering of the values is present at that distance.
Formula
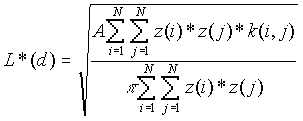 [1]
[1]
For![]() ,same as [1] except
,same as [1] except ![]() .
.
A
is the size of the study areaN is the number of points
d
is the distance  is the number of j points within distance d of all i points
is the number of j points within distance d of all i points
k(i,j) is the weight based on border effects. See the K-function section for
edge correction formulas.
Output
The output file lists the input data file name, the number of points, the minimum and maximum coordinates, the size of the study area, and the following tables showing L(d).
|
Distance (d) |
Observed L(d) |
Minimum L(d) |
Maximum L(d) |
|
: : : |
Limitation
The boundary correction formulas used here are inappropriate for irregular borders. In this program we assume the study area is a regular rectangle or square.
Example
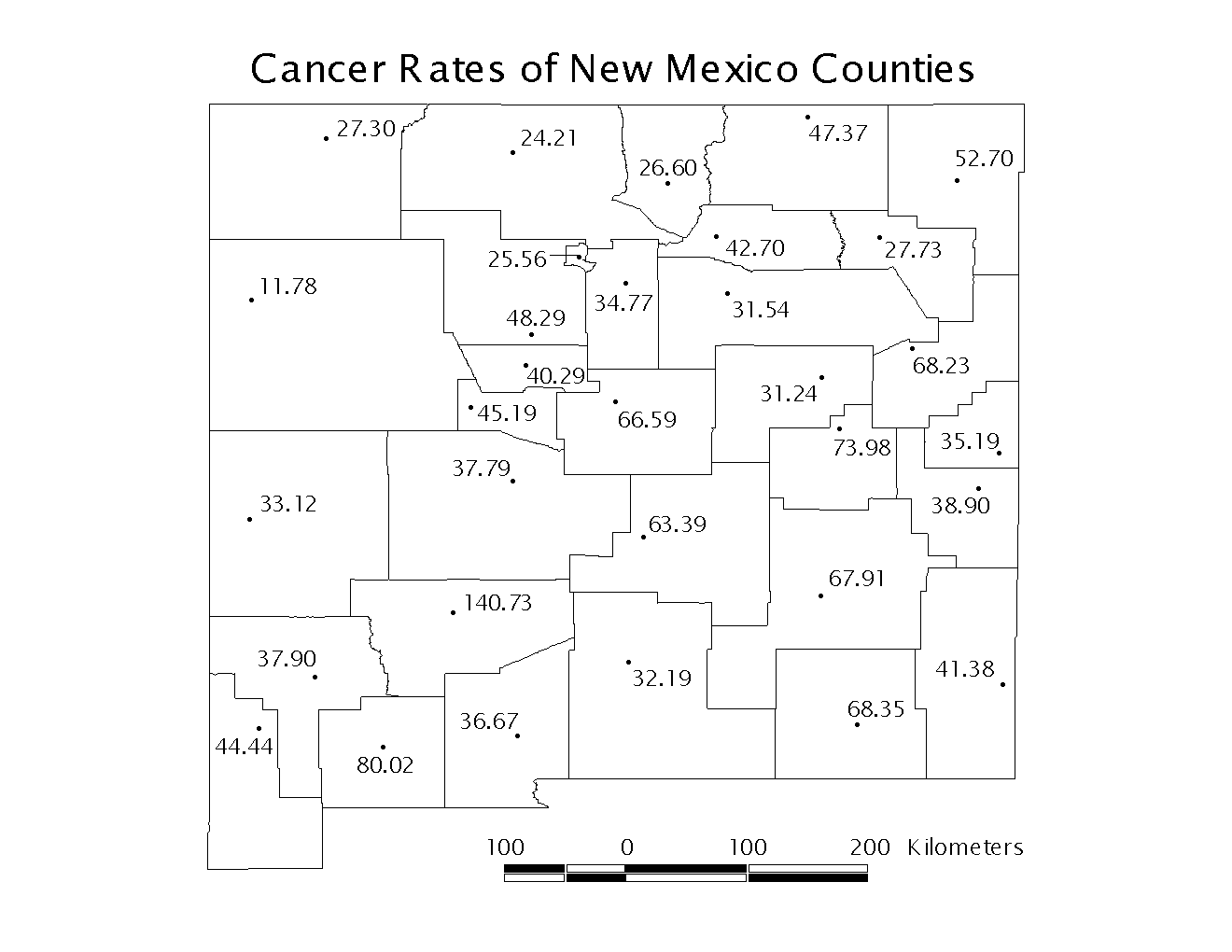
For this example we will consider lung cancer rates in the counties of New Mexico. The data are taken from the National Cancer Institute Biometry Research Group Datasets, and it is available on their website (http://dcp.nci.nih.gov/bb/datasets.html). The total number of cases diagnosed between 1980 and 1989 were divided by the 1985 population estimate to determine the lung cancer rate of each county. The rates are given in cases per 10,000 population. A sample of the input file is shown in Table 1. The statistically unbiased maximum distance is also approximately one half the length of the shortest side of the rectangular study area. New Mexico is approximately 500km per side, so we will set our maximum study distance at 250km. We will choose 25 increments so that we will calculate the observed L(d), observed L*(d), and confidence interval for every 10km. We use 99 permutations to create the confidence envelope in order to test the null hypothesis at the α=0.01 level.
Table 1: Input File
219 338 40.286 27 189 33.124 418 156 76.914 408 538 47.365 534 262 35.186 . . . . . . . . . 438 272 73.982
A map of the county seats and their corresponding rates is shown below in Figure 1. Please see the example of K-function analysis where we determined that the county seats are in a dispersed or regular pattern.
Figure 1: New Mexico County Seats
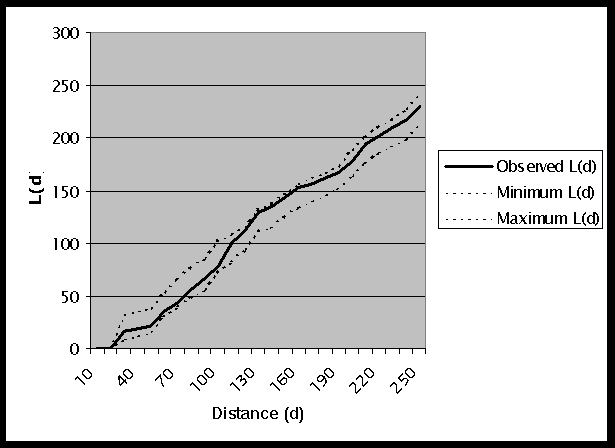
The complete output file for this weighted K-function analysis is shown in Table 2. Remember that L(d) does not include the interaction of each point with itself in the analysis, and this makes L(d) an indicator of the amount of spread of high values around each point. A graph of the results for L(d) is shown in Figure 2. Note that the values found for distances up to 20km are 0.000. This is due to the fact that there are no points within 20km of each other. For the remaining distances, the observed L(d) is within the confidence envelope. This indicates that the cancer rates are distributed in a random pattern within the dispersed pattern of points.
Figure 2: Graph of L(d) Results
L*(d), on the other hand, includes the interaction of each point with itself. A graph of the results of L*(d) is shown in Figure 3. The observed L*(d) values for distances of up to 30km are much higher than d. For all distances the observed L*(d) is within the generated confidence interval. This indicates that, although a particular site may have a high cancer rate, there is not clustering among the sites. We can not reject the null hypothesis of a random pattern of values in the already determined dispersed pattern of points. For further analysis of the same data, see the example using the Gi*(d) statistic.
Figure 3: Graph of L*(d) Results
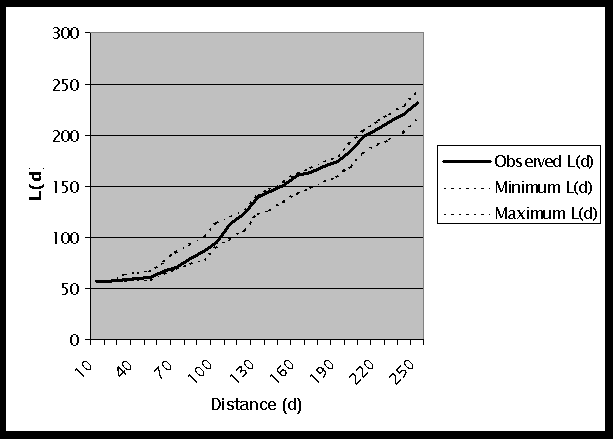
Table 2: Output File
The input data file: nmlung.txt
The total number of points: 32
The minimum x coordinate: 27.000000
The maximum x coordinate: 534.000000
The minimum y coordinate: 30.000000
The maximum y coordinate: 538.000000
The total area: 257556.000000
The maximum search distance: 250.000000
The step size: 10.000000
The number of permutations for the confidence envelope:99
Distance Observed L(d) Minimum L(d) Maximum L(d)
10.0000 0.0000 0.0000 0.0000
20.0000 0.0000 0.0000 0.0000
30.0000 16.3198 9.7937 32.3642
40.0000 19.2210 12.4469 35.0250
50.0000 20.9167 15.2865 37.4224
60.0000 35.9706 31.3370 52.8135
70.0000 43.8182 39.8616 66.5759
80.0000 55.7620 48.6995 76.9947
90.0000 66.1217 55.2053 85.7109
100.0000 78.4303 72.2880 101.9169
110.0000 100.6241 82.6214 109.3578
120.0000 111.9529 93.3499 115.2715
130.0000 128.8449 110.9001 131.7032
140.0000 135.6181 115.2361 139.2102
150.0000 143.6261 125.4658 146.5212
160.0000 153.1323 134.4913 156.2502
170.0000 156.9485 140.0888 162.1014
180.0000 162.9679 146.3413 167.6751
190.0000 167.7339 152.2540 173.0551
200.0000 178.1075 163.3612 188.0481
210.0000 194.2825 176.8804 201.1089
220.0000 201.9797 185.9301 210.7177
230.0000 209.7962 191.8762 218.1049
240.0000 217.0698 199.5325 227.1929
250.0000 229.6410 211.8279 241.0012
Distance Observed L*(d) Minimum L*(d) Maximum L*(d)
10.0000 56.8175 56.81748 56.81748
20.0000 56.8175 56.81748 56.81748
30.0000 59.0261 57.62260 65.07246
40.0000 59.8592 58.11241 66.38277
50.0000 60.4029 58.75969 67.62780
60.0000 66.8667 64.58767 76.86131
70.0000 71.2226 68.95364 86.52195
80.0000 78.8365 74.20567 94.46153
90.0000 86.1867 78.45916 101.41647
100.0000 95.5894 90.81857 114.91856
110.0000 113.8188 98.92281 121.31131
120.0000 123.5644 107.70001 126.46152
130.0000 138.4758 122.64893 141.03523
140.0000 144.5554 126.43053 147.79919
150.0000 151.8038 135.46233 154.43877
160.0000 160.4817 143.54054 163.34314
170.0000 163.9851 148.59448 168.73169
180.0000 169.5316 154.27477 173.88527
190.0000 173.9398 159.67690 178.87711
200.0000 183.5794 169.89481 192.86749
210.0000 198.7149 182.43610 205.13509
220.0000 205.9553 190.88464 214.20029
230.0000 213.3296 196.45609 221.18956
240.0000 220.2093 203.65094 229.80939
250.0000 232.1351 215.24963 242.94597
References
Getis, A. (1984) Interaction Modeling Using Second-order Analysis, Environment and Planning A 16: 173-183
National Cancer Institute Biometry Research Group Datasets
http://dcp.nci.nih.gov/bb/datasets.html