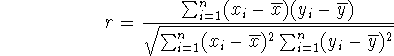
If we think of the ![]() and
and ![]() as components of vectors
as components of vectors ![]() and
and ![]() , then
, then
![]()
or
![]()
This is the inner product of two unit vectors, which is always between -1 and 1 (the inner product of two vectors is
![]()
where ![]() is the angle between the vectors (and hence always between -1
and 1). We can demonstrate this fact using linear algebra, calculus (and a
trick!) as follows:
is the angle between the vectors (and hence always between -1
and 1). We can demonstrate this fact using linear algebra, calculus (and a
trick!) as follows:
![]()
as this is the norm of the vector ![]() . Expanding
this product as a function of t, we get
. Expanding
this product as a function of t, we get
![]()
Since this is always positive ( ![]() ), there are no roots: hence, the
coefficients must satisfy the relationship
), there are no roots: hence, the
coefficients must satisfy the relationship
![]()
This works out to
![]()
or
![]()
QED
![]()
so
![]()
Thus
![]()
If we can show that the middle term is zero, we're done.
Recall that from our efforts to minimize ![]() we obtained two equations:
we obtained two equations:
![]()
and
![]()
Now
![]()
The second piece on the right hand side is clearly zero, as
![]()
The second piece is also zero, but requires a little more work: from the second equation above, we have that
![]()
Thus
![]()
then, using the second equation,
![]()
and so
![]()
QED