
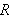 whose elements are the real numbers, with signature consisting of the
individual constant 0 to name the number zero, a 1-ary function symbol - for
minus, and two 2-ary function symbols + and
whose elements are the real numbers, with signature consisting of the
individual constant 0 to name the number zero, a 1-ary function symbol - for
minus, and two 2-ary function symbols + and

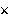 for plus and times. )
for plus and times. )
It is the current thesis of many mathematicians that set theory has now replaced geometry as the ultimate model for rigorous thought. They may be correct. Through set theory quite a number of problems have been resolved, and with derivatives of set theory such as model theory issues of our language itself can be shown to create many new problems that can be fully analysed within the context of language models.
Abraham Robinson was born on October 6 1918 in Waldenburg, Germany. Robinson's
family emigrated to Palestine in 1933. There Robinson studied mathematics
under Fraenkel. During World War II, he worked on aerodynamics. After the war
studied at London University, receiving his PhD in 1949. The area of his
dissertation was model theory. (Classical model theory, now called first-order
model theory, is a branch of mathematics that deals with the relationships
between descriptions in first-order languages and the structures that satisfy
these descriptions. A first-order language is formed by building up formulas
from the symbols in the signature, where the signature is a set of individual
constants, predicate symbols and function symbols; each of the predicate
symbols and function symbols has an arity (for example it is binary if its
arity is 2). For example the field of real numbers forms a structure

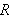 whose elements are the real numbers, with signature consisting of the
individual constant 0 to name the number zero, a 1-ary function symbol - for
minus, and two 2-ary function symbols + and
whose elements are the real numbers, with signature consisting of the
individual constant 0 to name the number zero, a 1-ary function symbol - for
minus, and two 2-ary function symbols + and

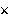 for plus and times. )
for plus and times. )
He is most famous for his contributions to what is called
nonstandard analysis, a variant of real analysis,
which allows actual infinitesimals and infinities --- without paradoxes. For
example, we can say the

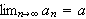 if
if

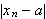 is an infinitesimal for every infinite value of
is an infinitesimal for every infinite value of

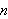 .
Achieving such a mathematics had long been sought but without success. Among
the many contributions of nonstandard analysis is a completely rigorous
calculus. There have even been written elementary books on calculus based on
nonstandard analysis. While a powerful tool, nonstandard analysis has not
caught on. In this brief chapter, we will consider some philosophical
observations of Robinson.
.
Achieving such a mathematics had long been sought but without success. Among
the many contributions of nonstandard analysis is a completely rigorous
calculus. There have even been written elementary books on calculus based on
nonstandard analysis. While a powerful tool, nonstandard analysis has not
caught on. In this brief chapter, we will consider some philosophical
observations of Robinson.
Robinson died of cancer on April 11, 1974 in New Haven,
Connecticut.
Commonly accepted: math as a deductive science begin with Greeks
4
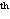 --5
--5
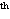 century B.C.
century B.C.
What about the Babylonian? the Egyptians? Was their mathematics not deductive?
What would the Babylonian mathematician say of Euclid?
Major discoveries were not the \underline{invention} of new math but the \underline{codification} of elements of mathematical thought -- explicit arguments notions assumptions rules etc. which had been intuitive for a long time.
| THEN: | One could know both. | |
| NOW: | It is very difficult to be dually conversant. |
Hence -- Plato or Aristotle or some other philosophical school could have influenced the development of the Axiomatic method even though none that we know of (except Democritus (atomism and math treatises) contributed to mathematics.
Aristotle established standards of rigor and completeness which went far beyond the level actually reached at that time.
Euclid and Archimedes singled out those axioms which could not be taken for granted and then proceeded to produce them with assumptions whose truth seemed obvious -- by means of rules of deduction seemingly equally obvious.
Yet Euclid did make the Archimedian Axiom as a definition because he didn't wish to exclude the other. He needed it for the theory of proportion and method of exhaustion.

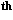 century) been regarded as statements of
century) been regarded as statements of 
 .
.However in Euclid there is an element of "constructivism" which should hark back to pre-Hellenic times and should strike a chord in the hearts of those believing Mathematics has been pushed too far in a formal-deductive direction and needs a more constructive approach in the foundations.
Ironic fate: only after Geometry lost its standing as the basis of all Mathematics was its axiomatic foundations finally reached the degree of perfection which the public estimation had always given them.
Soon thereafter the first form axiomatic theories were proposed.

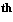 century:
century: Set theory achieves the position once occupied by Geometry.
The initial assumptions of Set Theory were held to be intuitively clear being based on natural laws of thought
Then Set Theory was put on a postulated basis including the axiom of choice (Zorn's lemma) the least intuitive At this point the axioms were still suppose to describe reality, although Platonic.
Then came the realization that it is equally consistent to deny or affirm some major assertions of Set Theory e.q. continuum hypothesis mid 1960s. This led to the end of Set Theory as describing objective reality.
Advances have been made through the codification of notion (e.g. truth). There is every reason to believe the codification will continue, bringing new advances.
Dictionary of Scientific Biography
A J Macintyre, Abraham Robinson 1918-1974, Bull. Amer. Math. Soc. 83
(1977), 646-666.
A D Young, S Kochen, S K-rner and P Roquette, Abraham Robinson, Bull.
London Math. Soc. 8 (1976), 307-323.
J W Dauben, Abraham Robinson : The Creation of Nonstandard Analysis,
a Personal and Mathematical Odyssey (Princeton, 1995).
G D Mostow, Abraham Robinson 1918-1974, Israel Journal of Mathematics
25 (1976), 4-14.
©2003, G. Donald Allen
This document created by Scientific WorkPlace 4.1.