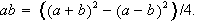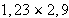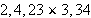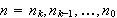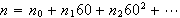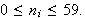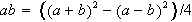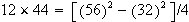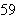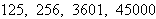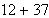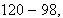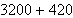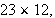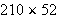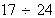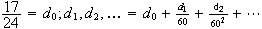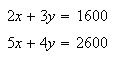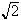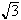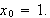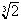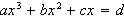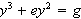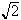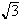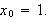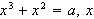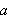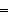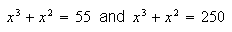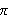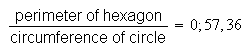-
Compute

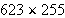 using the Egyptian binary algorithm.
using the Egyptian binary algorithm.
-
Compute

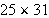 using the Egyptian binary algorithm.
using the Egyptian binary algorithm.
-
Compute

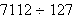 using the Egyptian binary algorithm.
using the Egyptian binary algorithm.
-
Show that if

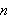 is a multiple of five,
is a multiple of five,

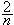 can be broken into the sum of two unit fractions, one of which is a third of
can be broken into the sum of two unit fractions, one of which is a third of

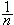 .
.
-
Solve

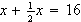 using the mathod of false position. Be sure to express the fractional answer
alá the Egyptians. (This is Proposition 16 of the Ahmes.)
using the mathod of false position. Be sure to express the fractional answer
alá the Egyptians. (This is Proposition 16 of the Ahmes.)
-
Solve the following problem using the method of false position: If thrice a
heep plus a fourth more is 247, what is the heep?
-
Devise a method by which the Egyptians may have found the formula for the
exact volume of a pyramid? (Remember, the formula can be computed by
calculus, but the Egyptians did not have that tool.)
-
The amount of bread to be distributed to four persons,

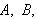 and
and

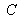 are in the continued proportions
are in the continued proportions

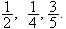 If there are 1200 loaves of bread to be distributed, how much does each get?
If there are 1200 loaves of bread to be distributed, how much does each get?
-
Solve the following problem using the method of false position: If thrice a
heep plus a fourth more is 247, what is the heep?
-
Using the Egyptian method find the area of a circle of diameter 11.
-
Pedagogy: Explain the issues of teaching mathematics by example, ála the
Ahmes Papyrus. What aspect make teaching this way simpler? harder? What kind
of graduate is the result of such instruction? (For example. Are graduates
capable? Are graduates flexible?)
-
Complete the checklist for Egypt by filling in the scaled numbers and
justifying by essay answers the values you have given. You may cite comments
or problems from the text or lecture notes; you may also contribute your own
observations.
-
Express the numbers 76, 234, 1265, and 87,432 in sexagesimal.
-
Compute the products. Use the product form

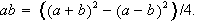
-

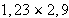
-

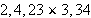
-
Convert the following numbers into sexagesimal and perform the computations in
sexagesimal. Perform the computations. Use here the form

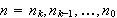 where
where

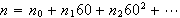 and all the
and all the

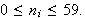 For multiplication use the form
For multiplication use the form

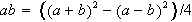 . For
example, in decimal
. For
example, in decimal

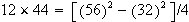 .
Remember the Babylonians had a table of squares up to
.
Remember the Babylonians had a table of squares up to

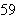 .
.
-

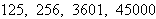
-

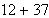 ,
,

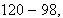

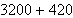
-

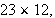

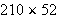
-
Determine

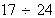 as a sexagesimal number. Here you need to use this form:
as a sexagesimal number. Here you need to use this form:

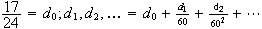
-
A problem on one Babylonian tablets give the base and top of an isosceles
trapezoid to be 50 and 40 respectively and the side length to be 30. Find the
altitude and area. Can this be done without the Pythagorean theorem?
-
Solve the following system ála the Babylonian "false position" method.
State clearly what steps you are taking.
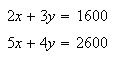
(The
solution is (200, 400).)
-
Generalize this Babylonian algorithm for solving linear systems to arbitrary
linear systems in two variables?
-
Generalize this Babylonian algorithm for solving linear systems to arbitrary
linear systems?
-
Modify the Babylonian root finding method (for

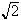 )
to find the square root of any number. Use your method to approximate
)
to find the square root of any number. Use your method to approximate

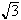 .
Begin with
.
Begin with

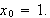 Compute five iterations.
Compute five iterations.
-
Explain how to adapt the method of the mean to determine

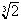 .
.
-
Show that the general cubic

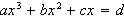 can be reduced to the normal form
can be reduced to the normal form

 .\
Determine Modify the Babylonian root finding method (for
.\
Determine Modify the Babylonian root finding method (for

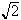 )
to find the square root of any number. Use your method to approximate
)
to find the square root of any number. Use your method to approximate

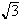 .
Begin with
.
Begin with

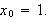
-
Consider the table:
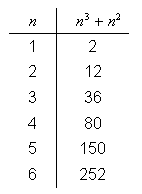
Solve the following problems using this table and linear interpolation.
Compare with the exact values. (You can obtain the exact solutions, for
example, by using Maple:
evalf(solve(
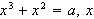 )). Here
)). Here

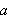

 the right
side.)
the right
side.)
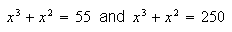
-
Derive the approximate value of

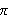 as determined from the data at Susa.
as determined from the data at Susa.
That is, show how the perimeter
identity
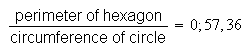
is
used to derive the approximation for

 .
.
-
Factor the other quadratic forms ála the Babylonian methods. You may use
variables, but not general formulas.
-
Complete the checklist for Mesopotamia by filling in the scaled numbers and
justifying by essay answers the values you have given. You may cite comments
or problems from the text or lecture notes; you may also contribute your own
observations.
-
Pedagogy: Explain the issues of teaching mathematics when clay tablets are
used for written communication. What difficulties do you perceive in teaching
the sexagesimal system? Using tables to solve nonlinear equations requires a
working knowledge of interpolation. Explain why interpolation is a naturally
occurring task in everyday life, even today.Write a lesson plan wherein you
show students how to

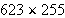 using the Egyptian binary algorithm.
using the Egyptian binary algorithm. 
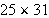 using the Egyptian binary algorithm.
using the Egyptian binary algorithm. 
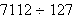 using the Egyptian binary algorithm.
using the Egyptian binary algorithm. 
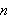 is a multiple of five,
is a multiple of five,

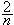 can be broken into the sum of two unit fractions, one of which is a third of
can be broken into the sum of two unit fractions, one of which is a third of

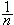 .
.

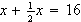 using the mathod of false position. Be sure to express the fractional answer
alá the Egyptians. (This is Proposition 16 of the Ahmes.)
using the mathod of false position. Be sure to express the fractional answer
alá the Egyptians. (This is Proposition 16 of the Ahmes.) 
 and
and

 are in the continued proportions
are in the continued proportions

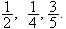 If there are 1200 loaves of bread to be distributed, how much does each get?
If there are 1200 loaves of bread to be distributed, how much does each get?