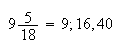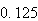 into the babylonian sexagesimal expression
into the babylonian sexagesimal expression

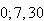 is answered thusly:
is answered thusly:
The question of converting

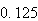 into the babylonian sexagesimal expression
into the babylonian sexagesimal expression

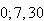 is answered thusly:
is answered thusly:
First, write

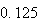 as a fraction:
as a fraction:

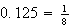
Now Babylonian sexagesimal numbers have the form
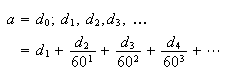
where

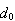 is the whole number portion of the number
is the whole number portion of the number

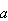 ,
and the other integers are the numerators of the fractions of the powers of
,
and the other integers are the numerators of the fractions of the powers of

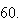
For

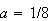 ,
it is clear that
,
it is clear that

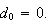 The numerator
The numerator

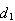 is determined as the largest integer such that
is determined as the largest integer such that
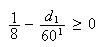
In
this case

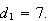 (Clearly, the next integer gives
(Clearly, the next integer gives

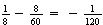 is negative.)
is negative.)
Now subtract to get
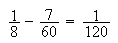
In general we now perform the same arithmetic with respect to the denominator

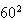 .
Thus we solve for the largest
integer
.
Thus we solve for the largest
integer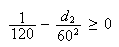

Since

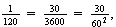 we conclude that
we conclude that

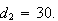 Also, there is no excess from the subtraction; so the process stops.
Also, there is no excess from the subtraction; so the process stops.
Here's another example. Find the sexagesimal representation of

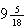
First

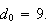 Now subtract
Now subtract

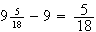 .
Solve for the largest integer
.
Solve for the largest integer

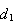 such
that
such
that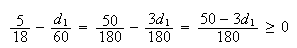
or

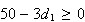 .
We see that
.
We see that

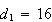 .
The difference
.
The difference

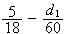 is therefore
is therefore

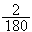 .
Since
.
Since

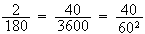

 we
see that
we
see that

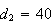 .Thus
we have exhausted powers of sixty needed. It follows that
.Thus
we have exhausted powers of sixty needed. It follows that