
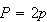 .
Thus
.
Thus

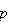 is the sum of the length and width. What is the area? Well, the two sides
is the sum of the length and width. What is the area? Well, the two sides

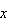 and
and

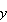 can be written as
can be written as
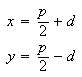
Thus the area is
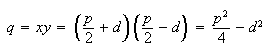
Solving we obtain
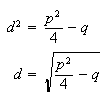
This gives
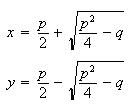
This is the form of the solution of the quadratic equation

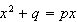 .
.
It has been conjectured by some authors, notably N. Katz, A History of Mathematics, that the origin of the quadratic formula may have resulted from the confusion between the knowing the perimeter and knowing the area of a rectangular region. Here is how the argument unfolds.
Suppose we know the perimeter of a rectangle to be

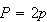 .
Thus
.
Thus

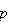 is the sum of the length and width. What is the area? Well, the two sides
is the sum of the length and width. What is the area? Well, the two sides

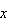 and
and

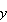 can be written as
can be written as
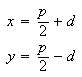
Thus
the area is
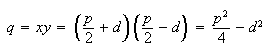
Solving
we obtain
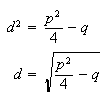
This
gives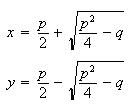
This
is the form of the solution of the quadratic equation

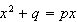 .
.
If it was the case that some people believe the area depended only on the perimeter, this gives a method of finding a variety of rectangles having the same perimeter but different areas. It is just conjecture, but one with a reasonable plausibility. In any event, the necessity of solving quadratics can arise from simple area calculations.
This document created by Scientific WorkPlace 4.1.