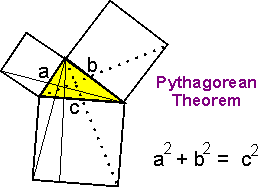
(The diagram to the left is that used by Euclid in his proof given 2300 years ago.)
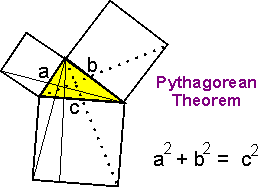 |
Arguably
the most famous theorem in all of mathematics, the Pythagorean Theorem has
an interesting history. Known to the Chinese and the Babylonians more than
a millennium before Pythagoras lived, it is a "natural" result
that has captivated mankind for 3000 years. More than 300 proofs are known
today. (The diagram to the left is that used by Euclid in his proof given 2300 years ago.) |
Exploring the concepts, ideas, and results of mathematics is a fascinating topic. On the one hand some breakthroughs in mathematical thought we will study came as accidents, and on the other hand as consequences of attempts to solve some great open problem. For example, complex numbers arose in the study of the solution of cubic polynomials. At first distrusted and ultimately rejected by their discoverers, Tartaglia and Cardano, complex numbers were subsequently found to have monumental significance and applications.
In this course you will see firsthand many of the results that have made what mathematics is today and meet the mathematicians that created them. One particularly interesting attribute of these "builders" of mathematical structure is how clear they were about what to prove. Their results turn out to be just what is needed to establish other results sometimes in an unrelated area. What is difficult to understand for the ordinary mathematics students is just how brilliant these people were and how tenaciously they attacked problems. The personality of the greatest mathematicians span the gamut from personable and friendly to arrogant and rude.
Nonetheless, it is the mathematics that is important. For the most part we will focus on the subject itself.
Each chapter contains goals, readings, and problems. You should begin by reading the goals of the chapter before the readings and answer the problems during and after reading the material. You will see this.
|
|
Goals
|
|
|
Readings
|
|
|
Problems
|
In most cases the reading will be presented in the form of Acrobat
(PDF) documents. To read and print them you will need the Adobe Acrobat Reader.![]()
The Goals and Problems will be given as HTML documents.
Web Mathematics History References
General References
There are many excellent
history of mathematics texts. Below we list several of them, though some are
topic specific. For supplementary reading, you should consider purchasing one
or more of these titles or borrowing them from your local library.
There are many other references. Please check with your instructor about the suitability of a particular source.