Day 49 in Mat229

• 5.3: The Divergence and Integral Tests
• 5.4 Comparison Tests
• 5.5 Alternating Series
• 5.6 Ratio and Root Tests
• 6.1 Power Series and Functions
  • Almost if by accident, we discover that we can represent functions as "power series" -- series made up of powers of \(x\) -- like infinite polynomials.

    But they may not work everywhere -- there's an "interval of convergence" for which they work, and we can find that (often with a ratio test).

    We then need to check the endpoints of the interval, to see if either should be included in the convergent interval.

  • Geometric series was featured, but we can then get other functions from that one: from \[ \frac{1}{1-x} = \sum_{n=0}^\infty x^n \] we got series for \(\frac{1}{1+x}\), \(\frac{1}{1-x^2}\), \(\frac{x}{1-x^2}\), etc. -- by composition.

• 6.2 Properties of Power Series
  • That we can add, subtract, and multiply power series to create new series (convergent on their shared open intervals of convergence)
  • We can also integrate and differentiate series to create series for other functions (on the open interval of convergence).

• 6.3 Taylor and Maclaurin Series
  • That we can create power series using Taylor's formula: given a function with infinitely many derivatives at \(x=a\), \[ f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!}(x-a)^k \] with an interval of convergence to be determined (often by a ratio test).

  • And if we approximate \(f(x)\) with the \(n^{th}\)-degree Taylor polynomial, then the error that we make in doing so is bounded by \[ |R_n(x)| \le \frac{M}{(n+1)!}|x-a|^{n+1} \] where \(M\) is a bound on the derivative \(f^{(n+1)}(x)\) on the interval between the center \(a\) and \(x\).

  • There are times to use Taylor's theorem, and there are times when you can move faster. Let's look at Exercise 6.15. Our author does this by Taylor's theorem first, but then suggests a better way....

• 6.4 Working with Taylor Series
  • The focus is especially on the binomial series, and more generally \[ (1+x)^r = \sum_{n=0}^{\infty} {r \choose n} x^n \] where \[ {r \choose n} \equiv \frac{r(r-1)\cdots (r-n+1)}{n!} \]
  • This table of Taylor series of common functions is good to review.

  • We also saw how we could integrate a series to provide a numerical approximation for a non-integrable function (e.g. the cumulative distribution function of the normal distribution)

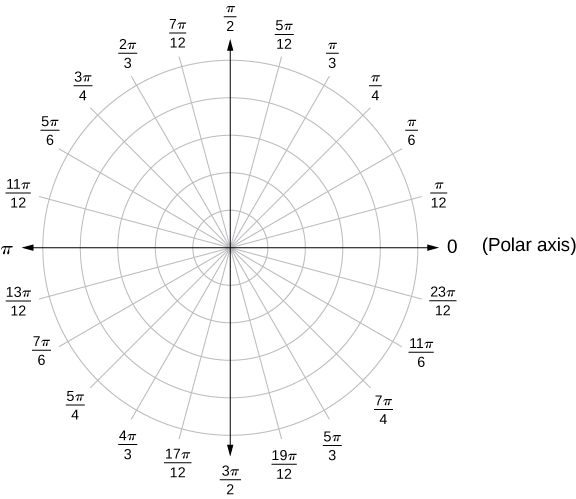
If \(r\) is the distance of a point \((x,y)\) from the origin, then we can write that

\[ x(r,\theta) = r\cos(\theta) \hspace{1in} y(r,\theta) = r\sin(\theta) \]

This section features some really beautiful curves that one can easily create using polar coordinates, such as the spiral inside a chambered nautilus:

• Polar Coordinates (.nb)
• Polar Coordinates (.pdf)
• Polar plotting example from our handout