- Return of quiz over 13.3
- The dot product detects perpendicular vectors: the dot product is zero.
- The dot product detects parallel vectors: the dot product is the product of their lengths.
- There will be a quiz today over the reading for 13.4.
- Remember to look over the exam again, correcting your errors, and see me for 40% of your missed points back.
- Homework for section 13.3 is due today (I'll post it, and your
quizzes, on my door tomorrow morning).
- Final exam:
- Tuesday, 1:00 p.m.
- Your final is comprehensive.
- It will be 40% recent material (chapter 13) and 60% will be material covered in our first two exams.
- A good strategy is to review your exams (for the older material), and the problems I assigned for homework.
- Reminder: we'll have a review session Monday evening, prior to the final. This will be question and answer, 7:00-9:00, in this room (if we need to move, I'll post a sign). Let me know if you'll be coming late....
- It's time for course evaluations. Please take the time to visit eval.nku.edu, and give me your feedback. Thanks!
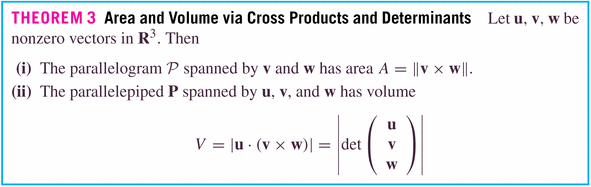
- The cross product, which is a product of two vectors resulting in a
third vector, which juts into the space perpendicular to which the two vectors
live.
It is only defined (and useful) in three-space, which makes it somewhat unusual (the dot product exists and is useful in any dimensional space).
The cross product is linear in its components: that is,
This means that we can define it on the unit vectors in three space, and then deduce it using the component-wise definition of a three-vector.
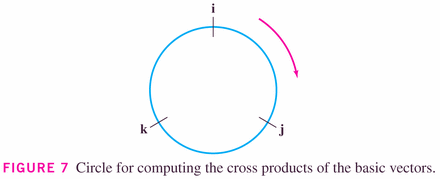
- #20, p. 691
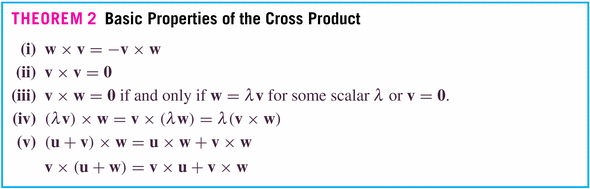
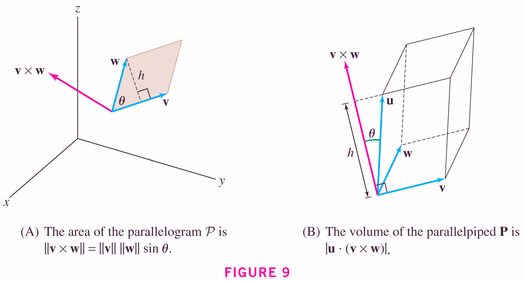
Now: here are the important geometric (rather than simply algebraic) properties of this product:

for the dot-product, it's the cosine; for the cross-product, it's the sine.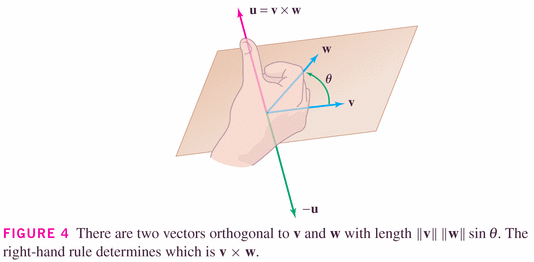
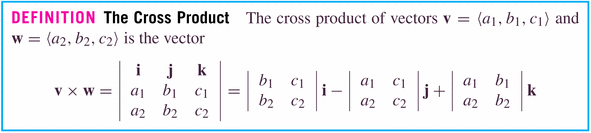
Example:
- #20, p. 691
Examples:
- #28, p. 691
- #46, p. 692
- The force
on a proton moving at velocity
(in m/s) in a uniform magnetic field
(in teslas) is
(in Newtons), where
Coulombs:
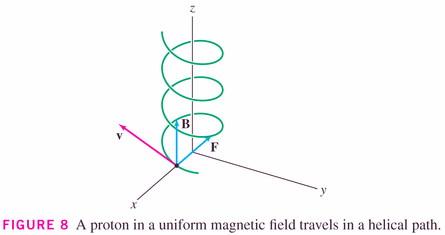
#36, p. 692
- Uniform magnetic field means that a particle experiences the same B-vector at every location.
- What can we say about the acceleration in the direction of B? Does the speed in the B-direction change?
- Application of the Cross-Product (see section 13.5 for more
details): Equations of Planes
- A few assignment problems:
- pp. 699--, #11, 13, 21, 31
- We'll start with planes through the origin: general planes
are just displaced versions of these.
- Thus, the vectors I discuss in the next few lines can be
considered position vectors, originating from the origin.
- The parallelpiped equation in Theorem 3

and
: We want to find all vectors
living in the space. Those will be the ones such that
I.e.,
creates a zero volume parallelpiped, because it's living in the plane of
and
.
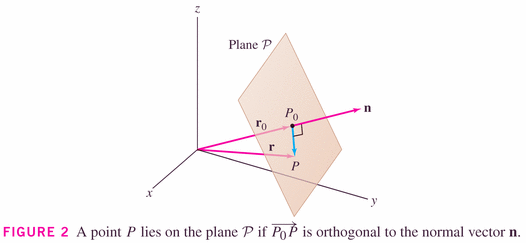
This gives us our first equation of a plane: if the coordinates of
are given by
and the coordinates of
are given by
(that is
is a normal vector) then the equation becomes
This is one form of the equation of a plane (through the origin). We say that the cross product
is normal to the vectors that live in the plane (or normal to the plane): that is, that it is perpendicular to the plane.
Notice that we can instantly see a normal vector to the vectors in the plane in this form: just pick off the coefficients of the variables (a, b, and c) and turn those into a normal vector.
Now (for the second equation!): notice that
satisfies the equation of the plane
, since
and
are both perpendicular to their cross product. Hence we have another (parametric) equation of a plane (through the origin):
- To offset these planes from the origin, one needs only reinterpret
in the two forms of the equation:
-
which leads to
where
-
which leads to
-
- Examples:
- #12, p. 699
- #29, p. 700
- #22, p. 700
- #30, p. 700
- A few assignment problems: