- Homework for 11.7 due today
- Exam revisions graded: come in to discuss it and get 100% on the redo. Email me to schedule a meeting (Please use subject line REDO).
- Short quiz on 13.1/13.2 today.
- Next week (Thursday) we'll have our second exam. It will cover the rest of chapter 11 (11.2-11.7).
- Uniform Circular Motion is best understood using the concepts of vector geometry.
So are many other concepts from physics, where quantities have a direction and a "strength" -- a rocket in flight, for example. It is moving in a certain direction, and it has a speed, whose value can be represented by the length of a vector.
- vector: a quantity with length and direction:
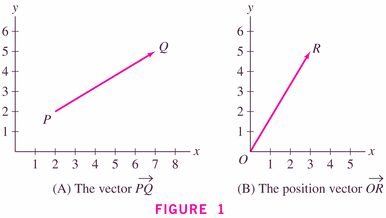
- In uniform circular motion, we could represent the position of the bob by
and
- The three vectors that are (most) important in the physics
of circular motion are the vectors of
- position,
- velocity, and
- acceleration,
- Animations, demonstrations:
- Uniform Circular Motion
- For all of the gory details, a nice layout of all the physics, and a cool (but scary) example, let's check out physclips -- the Australian dialect makes it more fun, too!
- vector: a quantity with length and direction:
- If a vector is in two-dimensions, then the length
is just given using the Pythagorean theorem formula:

in which case
Obviously this can be generalized to vectors in four dimensions, five dimensions; even six dimensions. Maybe seven dimensions, too; or even n dimensions.
- The vectors above are given with components:

examples:
- #5, p. 663
- #9, p. 663
- #11, p. 663

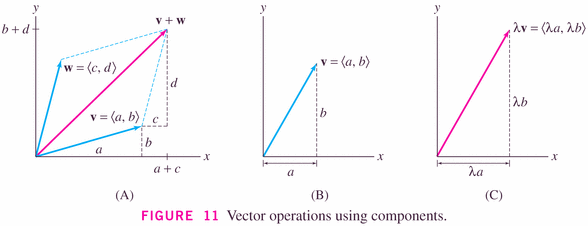
- Figure 11 illustrates the so-called parallelogram
rule:
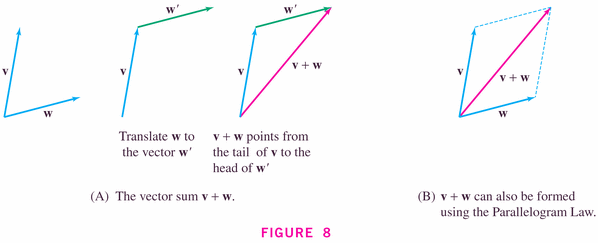
example:
- #17, p. 664
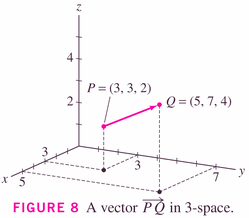
Here it is in three-space:
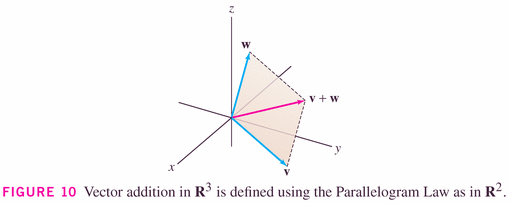
with the obvious changes to formulas because you now have three components, instead of two:
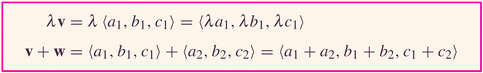
- Vectors with length 1 are special, called unit
vectors, and are important because they can be dedicated to
showing direction:
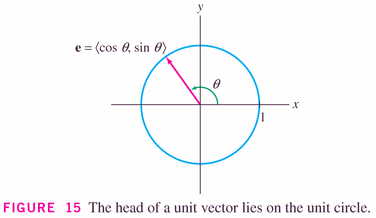
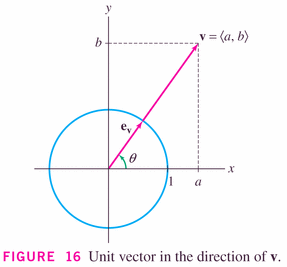
It's clear that we can turn any vector into a unit vector, by simply scaling it:

example:
- #38, p. 664
- We use special components and the parallelogram rule to
write each vector in terms of a basis of vectors (equal
in number to the dimension of the space): for example, in
two-space, the usual basis is given by the two (perpendicular)
vectors denoted i and j:
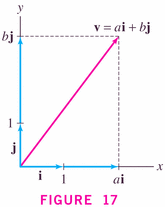
and, in three-space,
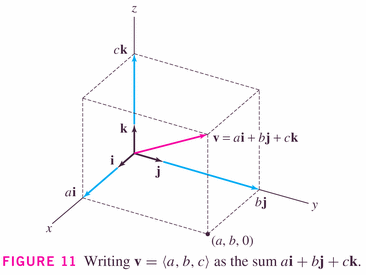
- Theorems:

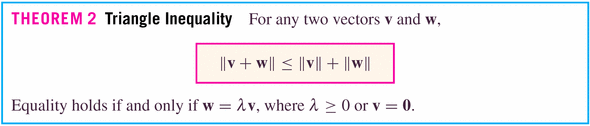
The Triangle inequality basically says that the diagonal of a parallelogram is shorter than or equal to the sum of the two sides:
"The shortest distance between two points is a straight line." In the case of Figure 17 (for vectors at right angles to each other)

and the only time you'll have equality is when either a or b is zero.
- Let's look at some more examples:
- #19, p. 664
- #29, p. 664
- #47, p. 664
- More physics:
- #58, p. 665
- First and foremost: Newton's laws of motion (in particular
), and statics.
- The parallelogram rule
- We can think of the force vectors on the cables as being composed of vector components (as well as coordinate components).
- First and foremost: Newton's laws of motion (in particular
- #60, p. 665
- Let's use a little calculus and the parameterization of the position vector in uniform circular motion given in one of our videos
- #58, p. 665
- The right-hand rule
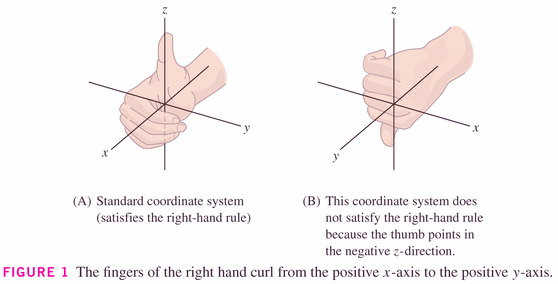
- Vocabulary:
- coordinate planes (p. 666)
- octants
- translates/translation (p. 669)
- parallel vectors
- equivalent vectors
- standard basis vectors
- Distance formula in R3:

examples:
- #1, p. 673
- #2, p. 673
- #14, p. 673
- Equations of Spheres and Cylinders
What are a sphere and a right cylinder?
- A sphere: all points equidistant from a given center.
- A right cylinder: all points equidistant from a given line.

examples: Draw the following:
- The set of points satisfying
- The set of points satisfying
- Parametric Equations of Lines:


- Additional examples:
- #27, p. 674
- #39, p. 674
- #51, p. 674