exactly, but when the
solution does not, in fact exist. The question then is, what's the best
non-solution? We need to do something, so what should we do when the
exact solution isn't a possibility? Do the next best thing....
Inner Product, Length, and Orthogonality
Summary
Our objective here is to solve the least squares problem: there are times when
we would like to the equation exactly, but when the
solution does not, in fact exist. The question then is, what's the best
non-solution? We need to do something, so what should we do when the
exact solution isn't a possibility? Do the next best thing....
What do we mean by ``next best thing''? We mean that we want to make the
distance between 
and 
as small as possible; that will
have to do with definitions of distance, which will fall out of something
called an inner product.
The classic example of this is the standard least-squares line, which students of any science are familiar with:
In terms of matrix operations, we're trying to find coefficients 
and
such that
for all points. Unfortunately, we have more than two points, so the system becomes over-determined:
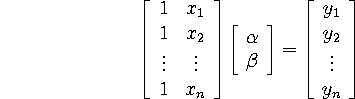
We can't (generally) find an actual solution vector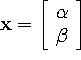 
that makes this true, so we make due with an approximate solution
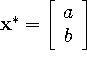that gives us a ``best fit'': that minimizes the distance between the two
vectors 
and 
.
inner product: The inner product between vectors u and
v in 
, or their dot product, is defined as
Example: #1, p. 382.
Properties of inner products (Theorem 1): Let u, v,
and w be vectors in , and c be any scalar. Then
, and
if and only if 
.
norm: The length or norm of vector 
is the
non-negative scalar 
.
Example: #7, p. 382.
unit vector: a vector whose length is 1 is called a unit vector, and one can ``normalize'' a vector (that is, give it unit length) by dividing the vector by its norm:
Example: #9, p. 382.
distance: For u and v in , the distance between u
and v, denoted dist(u,v), is the length of the vector
u-v. That is,
Example: #13, p. 382.
orthogonal: two vectors u and v in are
orthogonal (to each other) if and only if 
.
Example: #15, p. 382.
Theorem 2 (the Pythagorean Theorem): Two vectors u and v are orthogonal if and only if
orthogonal complement: If a vector z is orthogonal to every
vector in a subspace W of , then z is said to be orthogonal
to W. The set of all such vectors is called the orthogonal complement
of W, and denoted 
.
Example: #26, p. 383.
It is easy to deduce the following facts concerning the orthogonal complement of W:
if and only if x is orthogonal to
every vector in a spanning set of W. is a subspace of .
Demonstration: #29 and 30, p. 383
Theorem 3: Let A be an 
matrix. The orthogonal complement of
the row space of A is the nullspace of A, and the orthogonal complement
of the column space of A is the nullspace of 
:
The angle between two vectors in can be defined using the familiar
formula from calculus:
One interpretation of the cosine of this angle in higher dimensional space is as a correlation coefficient.
Example:
