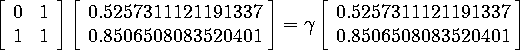Eigenvalues and Eigenvectors
Summary
We're considering the transformation ![]() . Eigenvectors provide the ideal basis for
. Eigenvectors provide the ideal basis for ![]() when considering
this transformation. Their images under the transformation are simple scalings.
when considering
this transformation. Their images under the transformation are simple scalings.
Eigenstuff: An eigenvector of ![]() is a nonzero vector
is a nonzero vector
![]() such that
such that ![]() . The scalar
. The scalar ![]() is
called the eigenvalue of A corresponding to
is
called the eigenvalue of A corresponding to ![]() . There may be
several eigenvectors corresponding to a given
. There may be
several eigenvectors corresponding to a given ![]() .
.
The idea is that an eigenvector is simply scaled by the transformation, so the
actions of a transformation are easily understood for eigenvectors. If we could
write a vector as a linear combination of eigenvectors, then it would be easy
to calculate its image: if there are n eigenvectors ![]() , with n
eigenvalues
, with n
eigenvalues ![]() , then if
, then if
![]()
then
![]()
Nice, no?
If ![]() is an eigenvalue of matrix A corresponding to eigenvector
is an eigenvalue of matrix A corresponding to eigenvector
![]() , then
, then
![]()
This means the
![]()
which is equivalent to
![]()
So ![]() is in the null space of
is in the null space of ![]() . If the null space is
trivial, then
. If the null space is
trivial, then ![]() is the zero vector, and
is the zero vector, and ![]() is not an
eigenvalue. Alternatively, all vectors in the null space are eigenvectors
corresponding to the eigenvalue
is not an
eigenvalue. Alternatively, all vectors in the null space are eigenvectors
corresponding to the eigenvalue ![]() .
.
As for determining the eigenvectors and eigenvalues, there is some cases in which this is extremely easy:
The eigenvalues of a diagonal matrix are the entries on its diagonal. More generally,
Theorem 1: The eigenvalues of a triangular matrix are the entries on its main diagonal.
Theorem 2: If ![]() are eigenvectors
corresponding to distince eigenvalues
are eigenvectors
corresponding to distince eigenvalues ![]() of an
of an ![]() matrix A, then the set
matrix A, then the set ![]() is linearly
independent.
is linearly
independent.
The eigenvectors and difference equations portion of this section can be illustrated with the example of the Fibonacci numbers transformation: recall that the Fibonacci numbers are those obtained by the recurrence relation
![]()
and ![]() and
and ![]() .
.
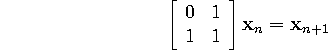
where

The eigenvalues of this matrix are approximately
![]() and -0.618033988749894.
and -0.618033988749894. ![]() is the so-called ``golden
mean'', which is a nearly sacred number in nature, well approximated by the
ratio of consecutive Fibonacci numbers.
is the so-called ``golden
mean'', which is a nearly sacred number in nature, well approximated by the
ratio of consecutive Fibonacci numbers.
An eigenvector corresponding to the golden mean (normalized to have a norm of 1) is approximately
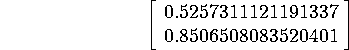
so that