We encounter yet another representation for a system of linear equations - will it never end?! This is the last we'll examine, and probably the most important. Theorem four pulls all these forms together: spans, pivots, linear combinations, and matrix equations collide!
``A fundamental idea in linear algebra is to view a linear combination of vectors as the product of a matrix and a vector.'' p. 40
Matrix/vector multiplication is defined. One form that I find particularly
useful is the so-called ``row-vector rule'': a row of the matrix slams into the
variable vector ![]() , to produce a single entry in the
, to produce a single entry in the ![]() vector.
vector.
Definition: product of matrix A and vector ![]()
If A is an m x n matrix, with columns ![]() ,
, ![]() ,
,
![]() , and if
, and if ![]() is in
is in ![]() , then the product of A and
, then the product of A and
![]() is the linear combination of the columns of A using the
corresponding entries in
is the linear combination of the columns of A using the
corresponding entries in ![]() as weights; that is,
as weights; that is,
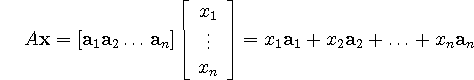
Example: #4, p. 47
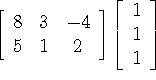
We now have four ways of writing a system of equations(!), as given in
Theorem Three (p. 42): If A is an m x n matrix, with columns
![]() ,
, ![]() ,
, ![]() , and if
, and if ![]() is in
is in
![]() , the matrix equation
, the matrix equation
![]()
has the same solution set as the vector equation
![]()
which, in turn, has the same solution set as the system of linear equations whose augmented matrix is
![]()
Example: #9, p. 47
![]()
Existence of solutions is given by the following theorem:
Theorem Four (p. 43): Let A be an m x n matrix. Then the following statements are logically equivalent. That is, for a particular A, either they are all true statements or they are all false.
Example: #14, p. 48
A handy way to think about matrix multiplication: Row-Vector rule for computing ![]()
If the product ![]() is defined, then the ith entry in the vector
is defined, then the ith entry in the vector
![]() (yes, it's a vector!) is the sum of the products of corresponding
entries from row i of A and from the vector
(yes, it's a vector!) is the sum of the products of corresponding
entries from row i of A and from the vector ![]() .
.
Example: Revisit #4, p. 47
Theorem Five (p. 45):
If A is an m x n matrix, ![]() and
and ![]() are vectors in
are vectors in
![]() , and c is a scalar, then:
, and c is a scalar, then:
Example: #35, p. 49