Section 1.3: Vector Equations

Abstract:

Vectors provide a wonderful way for us to write systems of equations compactly. You should already be familiar with two-d and three-d vectors from calculus classes. We now want to extend notions from those spaces into n-dimensional space. For example, vector addition is carried out component-wise.

The interesting new concept introduced in this section is that of span: roughly, the span of a set of vectors is the subspace generated by linear combinations of the vectors . The span represents the set of vectors that can be solutions of the system

Definition: A vector is a matrix with only a single column (``column vector''). The entries are called the components of the vector.

• zero vector: the vector whose components are all 0:
• one vector: the vector whose components are all 1:
• scalar multiple of a vector: a product of a constant (``scalar'') and a vector, the operation being carried out component-wise: e.g.

  

  Note: here's a notational issue. Vectors will generally be in bold-face (on the board I'll either underline them, or overline them, depending on my mood, time of day, and what I had for breakfast). The components of named vectors are generally written with the same name, only without bold/overline/underline, and with subscripts. Notice that the components of the vector above are not at all the same as the vectors listed in the abstract, . Components are (generally) numbers....

• vector sum: the vector created by adding two vectors, the sums being carried out component-wise. Naturally the vectors must have the same length....

  

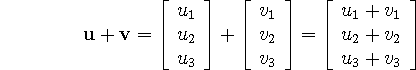
  Note: Geometrically, the sum of vectors can be found using the ``parallelogram rule'': the butt of vector is placed at the tip of the vector , and the vector from the butt of to the tip of is the sum.

• linear combination of vectors: any sum of vectors scaled by coefficients. E.g.,

  

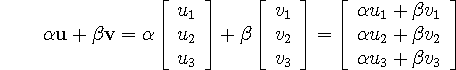
  Example: #4, p. 37

  

• span: the span of a set of vectors is the subspace generated by linear combinations of the vectors . The span represents the set of vectors that can be solutions of the system

  

  Q: What is the geometry of a span? What cases should be considered?

• The vector equation

  

  has the same solution as the linear system whose augmented matrix is

  

  In this case, the variables - the unknowns - would be the coefficients , and a solution would consist of the appropriate possibilities of values for those coefficients.

  Example: #9, p. 37

  

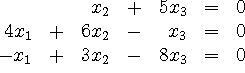
  Example: #12, p. 38. In this problem we throw you for another loop, by using the letter ``a'' for vectors! You have to pay attention, and not let us mess you up too badly just by poor notation....

  

• Two vectors are equal only if they have the same dimensions, and their components are the same.

• Algebraic properties of the vector space : for all u, v, w in and all scalars c and d,
  1. 
  2. 
  3. 
  4. 
  5. 
  6. 
  7. 
  8. 

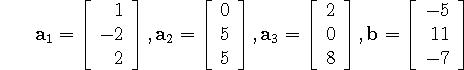
Example: #21, p. 38

Example: #27, p. 38