Approximating Integrals on the TIs
-
Define dd(n)=(b-a)/n
-
Define xx(k,n)=a+k*dd(n)
-
Define lrr(n)=dd(n)*
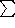 (f(xx(k,n)),k,0,n-1)
(f(xx(k,n)),k,0,n-1) -
Define rrr(n)=dd(n)*
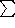 (f(xx(k,n)),k,1,n)
(f(xx(k,n)),k,1,n) -
Define trap(n)=(lrr(n)+rrr(n))/2
-
Define mx(k,n)=(xx(k-1,n)+xx(k,n))/2
-
Define mi(n)=dd(n)*
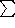 (f(mx(k,n)),k,1,n)
(f(mx(k,n)),k,1,n) -
Define simp(n)=(trap(n/2)+2*mi(n/2))/3
-
Define f(x) = .... Example: Define f(x)=1/x
-
left endpoint STO a Store the left endpoint as a
-
right endpoint STO b Store the right endpoint as b
Entering lrr(n), rrr(n), trap(n), mi(n) and simp(n) for a specific power of n yields the
approximating sums. For example, the approximating sums for the integral

for n=5 are
-
lrr(5)=.745635
-
rrr(5)=.645635
-
trap(5)=.695635
-
mi(5)=.691908
-
simp(10)=.693150
Note that the Simpson's Rule approximation is for the same integral with n=10.
-
For the Trapezoidal Rule:
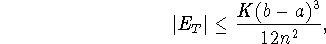
where K is an upper-bound for 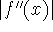 on [a,b].
on [a,b].
-
For the Midpoint Rule:
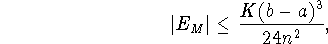
where K is an upper-bound for 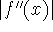 on [a,b].
on [a,b].
-
For Simpson's Rule:
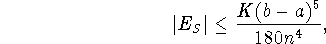
where K is an upper-bound for 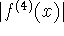 on [a,b].
on [a,b].
Upper-bounds might be determined algebraically, estimated graphically, or
derived from max/min considerations.
Wed Sep 3 18:28:23 EDT 2003
![]()
![]()
![]() on [a,b].
on [a,b].![]()
![]() on [a,b].
on [a,b].![]()
![]() on [a,b].
on [a,b].