-
exponential function: a function of the form

where a>0 is constant.
This is easy to understand when x is an integer, and makes a certain amount of sense for rational values of x (e.g.
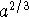 is the cube root of the
square of a. For real values of x, we can think of
is the cube root of the
square of a. For real values of x, we can think of 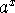 as
as

-
laws of exponents: (see the first theorem below)
-
e: the number such that

e is one of the two most important irrational numbers (along with
 ). An
irrational number has a non-repeating decimal representation.
). An
irrational number has a non-repeating decimal representation.
-
If a>0 and
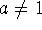 , then
, then 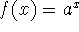 is a continuous function with domain
is a continuous function with domain
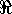 and range
and range 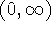 . In particular,
. In particular, 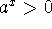 for all x. If 0<a<1,
for all x. If 0<a<1,
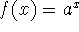 is a decreasing function; if a>1, f is an increasing
function. If a,b>0 and
is a decreasing function; if a>1, f is an increasing
function. If a,b>0 and 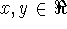 , then
, then
-
-
Some important limits:
-
If a>1, then
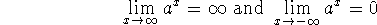
-
If 0<a<1, then
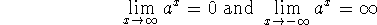
-
If a>1, then
-
For the natural exponential function with base e,

This is an amazing property: a function is its own derivative. That means that if you know its value at x, then you know the slope of the function there as well. The only other function with this property is the trivial function y=0. For this reason, the base e gives rise to what we call the natural exponential function.
Conversely, the function
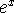 is its own antiderivative:
is its own antiderivative:

By the chain rule we get

which means that it's easy to differentiate the natural exponential function. The properties of the natural exponential function are easily deduced from those given above (
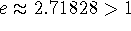 ).
).
There are three kinds of exponential graphs: increasing (a>1), constant (a=1), and decreasing (a<1).
The exponential function is crucial for many areas of study, from business (where the stock market and your bank account grow exponentially), to biology (populations grow exponentially at times of their life cycles), to all other areas of science.
The most important base of an exponential function is ![]() . We'll see that one can represent any exponential function, no matter
what the base, using e. The exponential function with e as its base is
called the natural exponential function: it has the amazing property that
the function is its own derivative and antiderivative.
. We'll see that one can represent any exponential function, no matter
what the base, using e. The exponential function with e as its base is
called the natural exponential function: it has the amazing property that
the function is its own derivative and antiderivative.