-
definite integral of f from a to b:
The definite integral of f from a to b is defined by
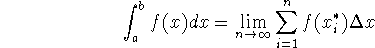
where the
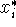 are sample points, one from each of the n rectangles of
width
are sample points, one from each of the n rectangles of
width 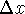 .
.
This looks like the area definition from section 5.1, but in that case the area has to be positive. Not so for the definite integral.
Integral sign:
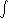 (due to Leibniz) - an elongated S,
representing a sum. Integration is just summation of an infinite number of
things!
(due to Leibniz) - an elongated S,
representing a sum. Integration is just summation of an infinite number of
things!
integrand: f(x) in the formula above - the function being integrated
limits of integration: a and b above - they represent the endpoints of the interval over which we are integrating. a is the lower limit and b is the upper limit, due to their position in the formula

infinitesimal: dx is an infinitesimal, having no finite length, but having the same units as x. It represents the infinitely fine width of the approximating rectangle of height f(x), so that f(x)dx is an area (albeit an infinitely small one!). The cool thing is that adding up an infinite number of infinitely small things can give a finite, non-zero answer!
-
Riemann sum: the sum

named after Bernhard Riemann (1826-1866), a student of Gauss.
-
Midpoint rule
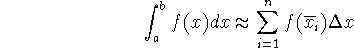
where

and
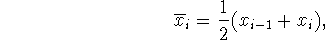
the midpoint of the
 subinterval
subinterval  .
.
-
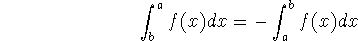
-

-
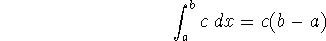
-
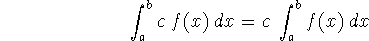
-
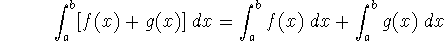
-
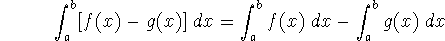
-
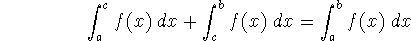
-
If
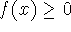 for
for 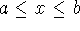 , then
, then

-
If
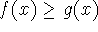 for
for 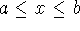 , then
, then
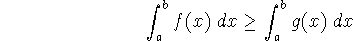
-
If
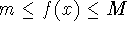 for
for 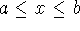 , then
, then
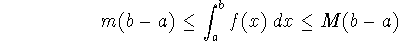
-
While we find it convenient to work with subintervals of equal width, there is
no need to, and we sometimes use subintervals of varying widths. In that case,
the formula for the Riemann sum might be written

and for the definition of the integral we would require that both
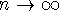 , and
, and 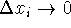 as
as 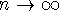 .
.
Whew! There's a lot going on in this section. The main idea is that we generalize from area to the integral, which is a way of defining the net area (i.e., some area is considered positive, and some negative; the integral is the sum of both parts for any function). Regions trapped between the curve of f and the x-axis, but above the x-axis, are considered positive in area; those below the x-axis are considered negative.
The integral of a function is a linear operation - that is, if
![]()
is integration (taking a function f and returning a number v), then if I(f) = v and I(g) = w we have that
![]()
We are introduced to the midpoint rule, which is an improvement on
either the right or left endpoint rules. While subintervals are generally of
fixed width ![]() , it is not necessarily so, and may sometimes be more
convenient to use variable sized rectangles.
, it is not necessarily so, and may sometimes be more
convenient to use variable sized rectangles.