- concave upward on interval I: the graph of f lies above all of its tangents on the interval I.
- concave downward on interval I: the graph of f lies below all of its tangents on the interval I.
-
inflection point: Point P on a curve is an inflection point if the
curve changes concavity at P.
``There is a point of inflection at any point where the second derivative changes sign.'' (p. 244)
-
Increasing/Decreasing Test:
If
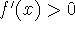 on [a,b], then f
increases on [a,b];
on [a,b], then f
increases on [a,b];
if
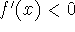 on [a,b], then f
decreases on [a,b].
on [a,b], then f
decreases on [a,b]. -
The first derivative test: Let c be a critical number of continuous
function f.
If
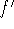 changes sign from positive to negative at c, then f has a
local maximum at c.
changes sign from positive to negative at c, then f has a
local maximum at c.
If
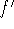 changes sign from negative to positive at c, then f has a
local minimum at c.
changes sign from negative to positive at c, then f has a
local minimum at c.
If
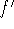 does not change sign at c, then f has neither a max nor a min
at c.
does not change sign at c, then f has neither a max nor a min
at c. -
Concavity test:
If
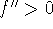 for all x in interval I, then f is
concave up on I;
for all x in interval I, then f is
concave up on I;
if
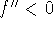 for all x in interval I, then f is
concave down on I.
for all x in interval I, then f is
concave down on I.
Just remember the two types of parabolas: bowls and umbrellas. Bowl:
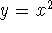 ,
so
,
so 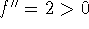 , and the curve is concave up; umbrella:
, and the curve is concave up; umbrella: 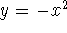 ,
so
,
so 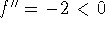 , and the curve is concave down.
, and the curve is concave down. -
Second derivative test: Suppose
 is continuous near
c.
is continuous near
c.
If
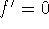 and
and 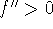 , then f has a local
minimum at c;
, then f has a local
minimum at c;
If
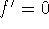 and
and 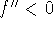 , then f has a local
maximum at c.
, then f has a local
maximum at c.
The second derivative test is inconclusive if
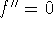 .
.
You'll notice that there are some nice tables which are created to show the sign of the derivative and hence indicate the direction (increasing/decreasing) of the function's graph; this is a graphing aid.
Knowledge of ![]() and
and ![]() inform us about critical aspects
of f (increasing/decreasing, extrema, points of inflection, concavity).
inform us about critical aspects
of f (increasing/decreasing, extrema, points of inflection, concavity).