Consider a set of data values of the form 
. We
think of y as a function of x, i.e. 
, and seek to
estimate the optimal parameters 
of the model
. For example, f might be parameterized by a slope m
and an intercept b, as in
Then would be the vector
We anticipate the presence of error, often assumed to be of the form
The upshot is that the error makes the data straddle the line (rather than fit it exactly).
We generally try to find the parameters using the principle of ``least squares'': that is, we try to minimize the ``sum of the squared errors'', or the function
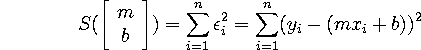
If we take partial derivatives of this expression with respect to the parameters, and set them to zero, we obtain two equations:
They look a lot simpler in vector form, however:
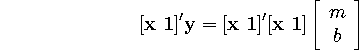
If we define
and write the vector of parameters as , then we can write the
system more succinctly as
With any luck, the matrix product X'X is invertible, so, formally, the parameters are estimated to be
This form readily generalizes, of course, to the case where there are p
independent predictor variables, rather than the single variable x. If we
include the ``one vector'' 
, then we will have an intercept term in
the linear model; otherwise, no.