
We show possible responses to parts (a) and (b) in Figures A2 and A3, respectively. These figures illustrate two different ways to represent a sequence graphically, by plotting successive points on a number line, and by plotting terms as a function of the subscript. We have used the latter representation for sequences many times. The former is introduced here as a way to visualize partial sums squeezing down on a limiting value.

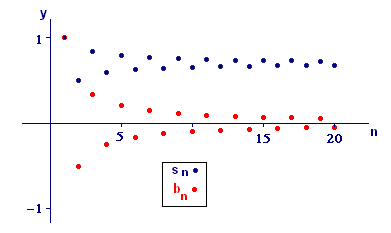
Both figures suggest that odd-numbered partial sums decrease and even-numbered ones increase as `n` increases. We can see that algebraically in the following way. Each partial sum is obtained from the previous one by adding one more term: `s_n =s_(n+1) + b_(n+1)`. At the next step, the same formula becomes `s_(n+2) =s_(n+1) + b_(n+2)`. Thus, to get from `s_n` to `s_(n+2)`, we first add `b_(n+1) = text[(]-1text[)]^n text[/] text[(] n+1 text[)]` and then add `b_(n+2) = text[(]-1text[)]^(n+1) text[/] text[(] n+2 text[)]`. If `n` is odd, then `1 text[/] text[(] n+1 text[)]` is being subtracted to get to `s_(n+1)`, and `1 text[/] text[(] n+2 text[)]` is being added to get to `s_(n+2)`. The amount being added is smaller than the amount being subtracted, so the next odd-numbered partial sum must be smaller. The argument for even-numbered sums is similar.
In general, the pattern for consecutive sums is that you jump down on even-numbered steps and back up on odd-numbered steps, with each jump being smaller than the one before it. Specifically, the size of the jump at step `n+1` is
`text[|] s_(n+1) - s_n text[|] = text[|] b_(n+1) text[|] = 1/(n+1)`,
which approaches `0` as `n rarr oo`. This shows that the even-numbered and odd-numbered sums steadily approach each other — that there is no "room" between them — so the sequence of partial sums must actually squeeze down on a limiting value `S`. Furthermore, because the sequence of even-numbered sums increases, `S` must be bigger than every even-numbered sum. Similarly, `S` must be smaller than every odd-numbered sum. At step `n`, if `n` is odd, then `s_(n+1) < S < s_n`, so
`text[|] S - s_n text[|] < text[|] s_(n+1) - s_n text[|] = 1/(n+1)`.
At an even-numbered step, `s_n < S < s_(n+1)`, but the conclusion is the same.