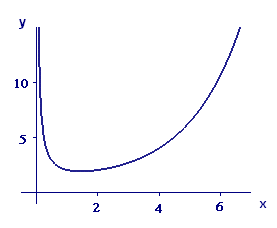
We show the graph of `f text[(] x text[)] = 2^xtext[/]x` in Figure A1.

This graph suggests that the function has a local minimum between `1` and `2`, and thereafter its values get steadily bigger as we go to the right. Furthermore, it appears that the graph is always concave upward, which means it can't level out as `x` gets large. Thus `f text[(] x text[)] rarr oo` as `x rarr oo`. Now the values of `2^m//m` are values of `f` at integer values of `x`, so we conclude that
`lim_(m rarr oo) 2^m/m = oo`.
If we substitute `m=k+1` in this formula, it tells us that the terms of the series in part (c) grow without bound (in absolute value) as `k rarr oo`. Thus, after the first few terms, we are alternately adding and subtracting larger and larger numbers. The effect of this is to generate partial sums that oscillate wildly — in particular, sums that cannot possibly settle down to a limiting value. We show the first 10 of those sums in Table 1.
| k | kth term | kth sum |
0 |
2 |
2 |
1 |
-2 |
0 |
2 |
2.667 |
2.667 |
3 |
-4 |
-1.333 |
4 |
6.4 |
5.067 |
5 |
-10.667 |
-5.6 |
6 |
18.286 |
12.686 |
7 |
-32 |
-19.314 |
8 |
56.889 |
37.575 |
9 |
-102.4 |
-64.825 |
What you should have observed by now in our examples of infinite series is that there is no hope of getting a finite sum from infinitely many terms unless those terms get small. That is, in order for `sum_( ) b_k` to converge, we must have `b_k rarr 0` as `k rarr oo`. Since the terms of the series in Activity 1 do not approach zero, the series cannot have a finite sum.