If we write `ftext[(]xtext[)] = text[(]1 - xtext[)]^(-1)` we can quickly find derivatives from the Power Rule and Chain Rule:
| `f^'text[(]xtext[)]` | `= text[(]-1text[)(]1 - xtext[)]^(-2)text[(]-1text[)] = text[(]1 - xtext[)]^(-2),` |
| `f^('')text[(]xtext[)]` | `=text[(]-2text[)(]1 - xtext[)]^(-3)text[(]-1text[)] = 2 text[(]1 - x text[)]^(-3),` |
| `f^(''')text[(]xtext[)]` | `= text[(]-3text[)(]1 - xtext[)]^(-4) text[(]-1text[)] = 3! text[(]1 - x text[)]^(-4),` |
and so on. In general, we find that `f^((k))text[(]xtext[)] = k! text[(]1 - xtext[)]^(-(k+1))`, so `f^((k))text[(]0text[)] = k!`. Since `c_k = f^((k))text[(]0text[)/]k!`, it follows that every coefficient in every Taylor polynomial is `1`, i.e., the polynomials are `1`, `1 + x`, `1 + x + x^2`, ..., `1 + x + x^2 + x^3 + x^4 + x^5`.

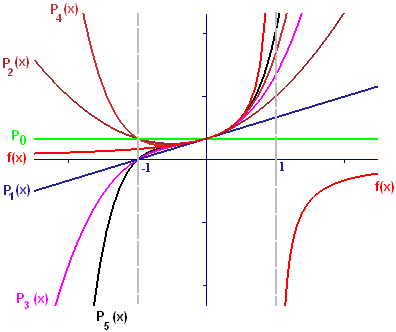
The graphs in Figure A1 suggest that the Taylor approximations are not very good near the endpoints of the interval `[-1,1]` and the polynomials are not approximations at all outside that interval. In Table A1 we show the requested values of the various functions at numbers near these endpoints. The numbers in the `0.9` and `-0.9` rows are consistent with the assertion that
but they are not very compelling evidence. The convergence is evidently very slow. The remaining rows show that, for `x ≥ 1` or `x ≤ -1`, the polynomial values have nothing to do with values of `ftext[(]xtext[)]`.
| `x` | `P_0` | `P_1text[(]xtext[)]` | `P_2text[(]xtext[)]` | `P_3text[(]xtext[)]` | `P_4text[(]xtext[)]` | `P_5text[(]xtext[)]` | `ftext[(]xtext[)]` |
0.9 |
1 |
1.9 |
2.71 |
3.44 |
4.10 |
4.69 |
10.0 |
-0.9 |
1 |
0.1 |
1.0 |
0.27 |
0.93 |
0.34 |
0.53 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
(no value) |
-1 |
1 |
0 |
1 |
0 |
1 |
0 |
0.5 |
1.1 |
1 |
2.1 |
3.31 |
4.64 |
6.11 |
7.72 |
-10.0 |
-1.1 |
1 |
-0.1 |
1.11 |
-0.22 |
1.24 |
-0.37 |
0.48 |