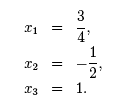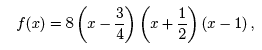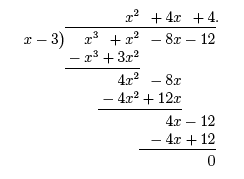Polynomial Functions
Polynomial division
|
As its name implies, polynomial division is the operation of dividing polynomials. It is used to find roots of polynomials and simplify rational functions. We will first present the method, and then detail its uses. To begin, consider the following expression,
As you can see, the expression is a fraction where the numerator and denominator are polynomials. As with fractions, the numerator of the above expression is called the dividend and the denominator is called the divisor. When we divide polynomials, the result is called the quotient which may or may not be accompanied by a nonzero remainder. We can divide the above polynomials using long division as follows, We will take this process step-by-step. The first thing to do is, Step 1: Line up the the dividend in descending power order. If any of the powers of x are missing, leave blank space where they would be. Step 2: Ask yourself: “What times the first term of the divisor equals the first term of the dividend ?” The answer to this question is the first term of the quotient.
Step 3: Multiply the first term in the quotient by the divisor.
Step 4: Subtract the result from the dividend. You only need to worry about the terms in the dividend that are of the same power as the result.
Step 5: Bring down the next term in the dividend and repeat the above process with the next highest power of x.
Polynomial division where the remainder is not zero. It is not always the case that the remainder is zero; we will see this more when we study rational functions and their asymptotes. We will now look at one such example. Now suppose we want to divide the following, This results in the following,
In this case, the dividend is missing a quadratic term, so we leave a blank space where it would be. We will again walk through the process of long polynomial division. First, we ask, “What times the first term in the divisor (x) equals the first term in the dividend (x3)?” Of course x2 times x equals x3, so x2 is the first term in the quotient. Next, we multiply x2 times the divisor to get x3− 2x2 and subtract this quantity from x3 + 0x2 to get 2x2, and we bring down the next term in the dividend (4x). Now, we ask, “What times x equals 2x2?” Since x times 2x equals 2x2, 2x is the second term in the quotient. We then multiply 2x times the divisor to get 2x2− 4x and subtract it from 2x2 + 4x to get 8x, and we bring down the next term in the dividend (−13). Finally, we ask, “What times x equals 8x?” Since 8 times x equals 8x, 8 is the third term in the quotient, and we multiply 8 times the divisor to get 8x−16. Subtracting 8x−16 from 8x−13 gives a remainder of 3. What to do with the remainder? Since we have a remainder, the division process resulted in the quotient plus one additional term, the remainder over the divisor. That is, we have, Factoring polynomials When a polynomial (P(x)) is divided by x − a, the remainder is P(a). This can be seen in the above example where P(x) = x3 + 4x − 13, a = 2 and, P(2) = (2)3 + 4 (2) − 13 = 3. We say that x − a is a factor of P(x) if and only if P(a) = 0. It is important to recognize that a factor of a polynomial indicates a root of a polynomial. In particular, if x − a is a factor of P(x) then x = a is a root of P(x). This can be seen in the first example,
In this example, x − 1 is a factor of P(x) = 8x3− 10x2− x + 3, and x = 1 is a root of P(x). Notice that P(1) = 8 · (1)3− 10 · (1)2− (1) + 3 = 0, proving that x = 1 is a root. Using the n factors of an nth-degree polynomial (i.e. x − x1, x − x2, . . . , x − xn) we can write P(x) in its factored form as, P(x) = an (x − xn) (x − xn-1) · · · (x − x2) (x − x1) , where an is the leading coefficient of the polynomial. For example, a cubic function with roots x = 2, x = −3, and x = −1 has factors x − 2, x + 3, and x + 1, and can be written as, P(x) = a3 (x − 2) (x + 3) (x + 1) . To find a3 we simply need to know a point that lies on the graph. For example, if we are given that (1, 16) lies on the graph of P(x) we can find a3,
and a3= -2. Therefore, we write the factored form of P(x) as, P(x) = −2 (x − 2) (x + 3) (x + 1) . The expanded form of P(x) is, P(x) = −2x3 − 4x2 + 10x + 12. Finding the roots of polynomials Polynomial division is useful for finding the roots of some polynomials. While the roots of a quadratic function, f(x) = ax2 + bx + c, can be found using the quadratic formula,
this is not the case for polynomials generally. However, suppose you have a cubic function and know one of its roots — this root may be given, you may have determined it graphically, or you may have guessed it. Using the corresponding factor, you can divide the cubic function by the factor and reduce the cubic function to a quadratic function with no remainder. Once you have reduced the polynomial to a quadratic, you can use the quadratic formula to find the remaining two roots. The first example of polynomial long division,
is a good example of finding the roots of a cubic by reducing it to a quadratic. In this case, x3 = 1 is a root (x − 1 is a factor), and we reduce the cubic 8x3 − 10x2− x + 3 to the quadratic 8x2− 2x − 3. We find the remaining two roots of this quadratic as, and
We can write this cubic in its factored form as,
where a3 = 8 is the leading coefficient. Repeated Real Roots Polynomials may have roots with multiplicities greater than one, which are known as repeated real roots. We say that x = a is a root of multiplicity k of the polynomial P(x) if (x − a)k is a factor of P(x) ((x − a)k will appear in the factored form of P(x)). For example, the quadratic function, f(x) = x2, has the double root, x = 0 since the factor x − 0 = x appears as a squared term. The cubic function, f(x) = x3 + x2− 8x − 12, has roots x = 3 (simple root) and x = −2 (double root). To see this, we can divide f(x) by the known factor x − 3 to get,
The quotient, x2 + 4x + 4, can be factored as, x2 + 4x + 4 = (x + 2)2. We write f(x) in its factored form as, f(x) = (x − 3)(x + 2)2, where you can see that x = 3 is a simple root, because the factor x − 3 is raised to the first power, and x = −2 is a double root, because the factor x + 2 is raised to the second power. Other polynomials have roots of even greater multiplicity. For example, the polynomial, f(x) = (x + 13)8, has root x = −13 of multiplicity 8. The multiplicity of a root affects the shape of the graph of a polynomial. ***** In the next section we will explore the graphs of polynomials. |
The Biology Project > Biomath > Polynomial Functions > Polynomial Division
Department of Biochemistry and Molecular Biophysics
The University of Arizona
March 2006
Contact the Development Team
http://www.biology.arizona.edu All contents copyright © 2006. All rights reserved.
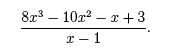
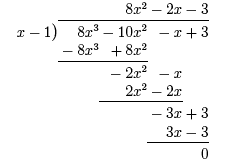
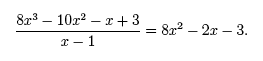
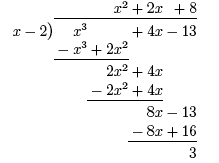
 You could also write + 0x2 if that is helpful to you.
You could also write + 0x2 if that is helpful to you. ![(x^3 + 4x -13)/(x-2) = x^2 + 2x + 8 + [3/(x-2)]](graphics/polydiveqn6.gif)
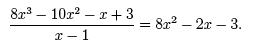

![x1,2 =[2 + or - the square root of (9-2)^2 -4(8)(-3))]/[2(*)] = (2 + or - 10)/16,](graphics/polydiveqn12.gif)