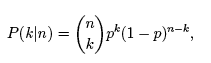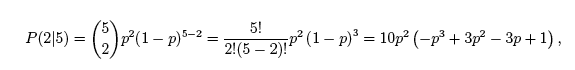Polynomial Applications
Binomial Distribution
Use the binomial distribution to answer the following questions: Write the binomial distribution for a given trial. Write the binomial distribution given the numbers of trials and number of successes Find the probability that a given number of offspring will be heterozygotes. Find the probability that given number of offspring will have genotype AA. Describe the shape of the graph of the binomial distribution.
***** |
||||
The Biology Project > Biomath > Polynomials > Applications > Binomial Distribution
Department of Biochemistry and Molecular Biophysics
The University of Arizona
March 2007
Contact the Development Team
http://www.biology.arizona.edu
All contents copyright © 2007. All rights reserved.