Trigonometric Functions
Trigonometric Identities
|
In this section we will briefly introduce some trigonometric identities. Identities are equations that are true for all values of the given variables. These identities are often used to simplify expressions and solve trigonometric equations. The following are groups of trigonometric identities, 1. Reciprocal Identities
2. Cofunction Identities (Radian Form)
3. Quotient Identities
4. Pythagorean Identities
5. Negative Angle Identities
6. Sum Identities
7. Difference Identities
8. Double Angle Identities
9. Product Identities
Using Trigonometric Identities These trigonometric identities are useful when you study integration, where the function you are trying to integrate can be greatly simplified using one of these identities. The sum and difference identities are also useful for finding the exact trigonometric functional value of an angle that can be expressed as the sum or difference of two special angles. For example, suppose you want to find the exact value of cos (π/12) . First, cos (π/12) in degree measure as, cos (15°). Notice that we can express 15° as the difference of two special angles, namely 45° and 30°. Therefore, we write, cos (15°) = cos (45° − 30° ) = cos (45 °) cos (30°) + sin (45°) sin (30°) ***** Now try some problems that will test your knowledge of trigonometric functions. |
The Biology Project > Biomath > Trigonometric Functions > Identities
Department of Biochemistry and Molecular Biophysics
The University of Arizona
April 2006
Contact the Development Team
http://www.biology.arizona.edu All contents copyright © 2006. All rights reserved.
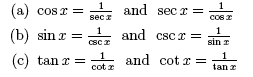
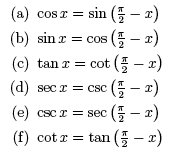
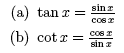
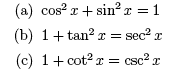
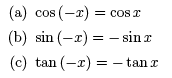
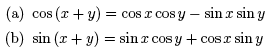
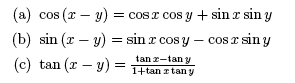
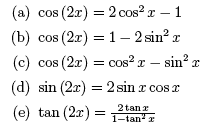
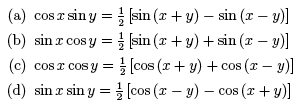
![=(square root 2/2)*[(square root 3/2) + 1/2]= (square root 6/4) + (square root 2/4) = [(square root 6) =2]/4.](graphics/trigidenteqn7.gif)