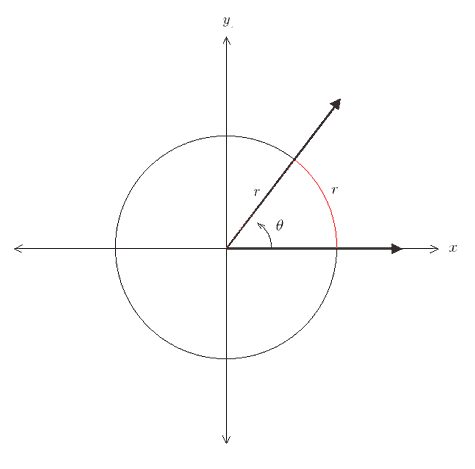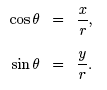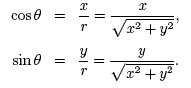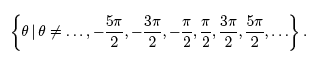Definition of the six trigonometric functions

We will begin by considering an angle in standard position.

The following diagram depicts an angle θ in standard position.

The rotation of an angle in standard position originates from the initial ray. Angles formed by counterclockwise rotation have positive measure, while angles formed by clockwise rotation have negative measure as pictured above. Two angles in standard position that have the same terminal ray are called coterminal. For example, the angles in the above figure are coterminal. Suppose we choose a point (x, y) ≠ (0, 0) lying on the terminal ray of an angle in standard position. If we let r be the distance from the origin to the point (x, y) then,

according to the distance formula. Using the variables x, y, and r, we define the six trigonometric functions as follows,

The six trigonometric functions are read as follows:

There are two important points to notice as you study these definitions. First, the the secant, cosecant, and cotangent functions are the reciprocals of the cosine, sine, and tangent functions, respectively. Second, there is no value for which the cosine and sine functions are undefined. This is because r is the distant from the origin to the point (x,y) ≠ (0,0) on the terminal ray.

Now let's apply these definitions to a real situation. Consider the following angle in standard position:

Using the above diagram, we compute r as,

We can now find the values of the six trigonometric functions with x = −4, y = 3, and r = 5 as,

Radian Measure

We have not specifically discussed the angle θ yet, but it can be measured in degrees or in radians. While you are probably comfortable with degree measure, you may be less so with radian measure. To define a radian, consider the following circle with radius r centered at the origin:

In the above picture, the angle θ has measure 1 radian. To be specific,

The radius and arc length in the above picture are equal (both equal r), so θ = 1. Likewise, if the radius of a circle is r and the central angle intercepts an arc length of 2r, then the central angle measures 2r/r = 2 radians.

Converting between degrees and radians

The angle corresponding to one complete rotation has measure 360 ° or 2π radians. To convert from degrees to radians or radians to degrees we simply use the following conversion factors:

2π radians = 360°
or π radians = 180°.

For example, if we want to convert x° to y radians, we simply write,

On the other hand, if we want to convert y radians to x°, we simply write,

To look at a concrete example, suppose we want to convert 512° to radians. Since we are going from degrees to radians, we set the conversion up so that degrees cancel,

In general, we will work with radian measure. Unless the degree unit (°) is explicitly written, all angles are assumed to be in radians.

Domain and Range of Trigonometric Functions

We will now discuss the domain and range of each trigonometric function. Remember that elements in the domain are valid inputs, in this case angle measurements, and elements in the range are the corresponding outputs. Outputs of the trigonometric functions are simply ratios of the variables x, y, and r. To begin, let’s look at the domain and range of the trigonometric functiony = cos θ and y = sin θ . Both of these trigonometric functions have domain all real numbers and range {y | − 1 ≤ y ≤ 1}. To determine the domain, we ask ourselves, "for what values of θ are cos θ and sin θ defined?" To answer this, recall the definitions of cos θ and
sin θ,

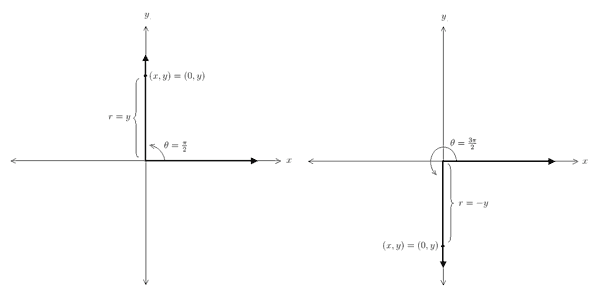
The ratios x/r and y/r are well defined provided r ≠ 0. Recall that r measures the distance from the point (x, y) ≠ (0, 0) lying on the terminal side of an angle in standard position to the origin. By definition, r cannot be zero. Thus, all values of θ are valid inputs.

To see that, {y| − 1 ≤ y ≤ 1} is the range of y = cos θ and y = sin θ, we need to inspect the ratios x/r and y/r . If we write r in terms of x and y we have,

Notice that Thus, cos θ = x/ r and sin θ = y/r cannot be greater than 1 or less than −1, depending on whether x and y are positive or negative (r = x when y = 0 and r = y when x = 0). So we conclude that the range of cos θ and sin θ is,

{y | − 1 ≤ y ≤ 1} .

The other trigonometric functions, specifically tan θ , sec θ , csc θ , and cot θ, contain an additional statement, either x ≠ 0 or y ≠ 0. We will use these restrictions to determine their domain and range. We will begin with y = tan θ = y / x . Notice that y / x is not defined when x = 0. Since x is the x-coordinate of a point lying on the terminal ray of an angle in standard position, we need to remove angles that correspond to points whose x-coordinate is zero. Points lying on the y-axis have x-coordinate equal to zero, so we must remove angles whose terminal ray lies along either the positive or negative y-axis. Two such angles are pictured below:

These two angles measure 90° (along the positive y-axis) and 270° (along the negative y-axis) corresponding to π/2 and 3π/2 radians. We also need to consider all coterminal angles by adding and subtracting multiples of 2π (e.g., π/2 + 2π = 5π/2 and π/2 − 2π = −3π/2 ). Therefore, we conclude that y = tan θ has domain,

The range of tan θ is easier to determine. Since y = tan θ = y / x , and y and x are coordinates of a point, y can be any real number and x can be any real number except 0. Thus, the ratio y / x can be any real number, and we conclude that the range of y = tan θ is all real numbers.

The domain of y = sec θ = r / x is the same as the domain of y = tan θ= y / x since x ≠ 0 in both cases,

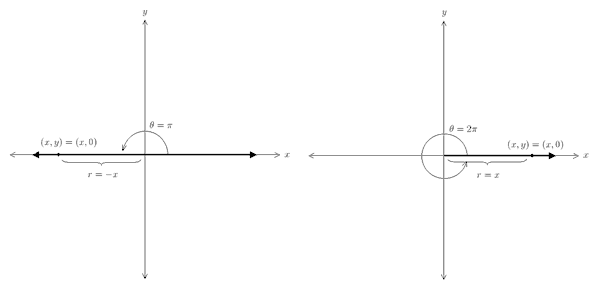
Knowing that the range of y = cos θ = x / r is {y | − 1 ≤ y ≤ 1}, we can easily find the range of
y = sec = r / x , since cos θ and sec θ are reciprocals of one another. Reciprocating changes the direction of inequalities in the range and we have,

{y | y ≤ −1 or y ≥ 1}.

To find the domain of y = csc θ = r / y , we notice that this function is not defined when y = 0. Since y is the y-coordinate of a point lying on the terminal ray of an angle in standard position, we need to remove angles that correspond to points whose y-coordinate is zero. Points lying on the x-axis have y-coordinate equal to zero, so we must remove angles whose terminal ray lies along either the positive or negative x-axis. Two such angles are pictured below:

These two angles measure 180° along the negative x-axis and 360° along the positive x-axis corresponding to π and 2π radians, respectively. Of course we also need to consider all coterminal angles by adding and subtracting multiples of 2π (e.g., π + 2π = 3π
and π − 2π = −π ). Therefore, we conclude that y = csc θ has domain,

{ θ| θ ≠ . . . ,−3π ,−2π ,−π , 0,π , 2π , 3π , . . .} .

Knowing that the range of y = sin θ= y / r is {y | − 1 ≤ y ≤ 1}, we can easily find the range of

y = csc θ = r/ y ,

since sin θ and csc θ are reciprocals of one another. Thus, the range of y = csc θ is,

{y | y ≤ −1 or y ≥ 1} .

The domain of y = cot θ = x / y is the same as the domain of y = csc θ = r / y since y ≠ 0 in both cases,

{θ | θ≠ . . . ,−3π ,−2π ,−π , 0,π , 2π , 3π , . . .}.

Using the same argument to find the range of y = tan θ, the range of y = cot θ is also all real numbers. The domains and ranges of the six trigonometric functions are summarized in the following table:

*****

In the next section we will find the trigonometric functional values of some special angles.

Special Angles