Rational Functions
Basics
|
Definition A rational function is a function of the form, where P(x) and Q(x) are polynomials. Some examples of rational functions include:
As you may have guessed, many of the functions we have studied so far fall into the broad class of rational functions. For example, some rational functions are power functions and vice versa. Polynomial functions are special cases of rational functions where Q(x) = 1 in the above definition. Domain and Range The domain of a rational function depends on the denominator Q(x). In particular, the domain of f(x) = P(x) / Q(x) is all real numbers x such that Q(x) ≠ 0. Notice that
we need to remove values of x that are zeros of Q(x) since division by zero is
undefined. For example, the domain of the function
It is not always possible to determine the domain of a rational function. For example, if Q(x) is of high degree we generally cannot find all of its zeros. In other cases, we can find the domain of f(x) = P(x) / Q(x) by finding the zeros of Q(x) as discussed in the sections on quadratic functions and polynomials. For example, the domain of the function,
consists of all real numbers x such that x2 − 6x + 3 ≠ 0. To determine which values of x to remove we set, x2 − 6x + 3 = 0, and solve for x using the quadratic formula as,
Thus, we conclude that the domain of,
is the set, {x | x ≠ 3 + √6 or x ≠ 3 − √6}, or using interval notation, (−∞, 3 − √6) ∪ (3 − √6, 3 + √6) ∪ (3 + √6, ∞) . ***** In the next section we will learn about asymptotes of rational functions. |
The Biology Project > Biomath > Rational Functions > Basics
Department of Biochemistry and Molecular Biophysics
The University of Arizona
April 2006
Contact the Development Team
http://www.biology.arizona.edu All contents copyright © 2006. All rights reserved.

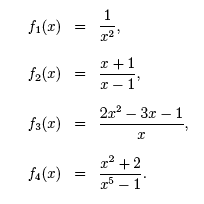
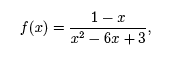
![x(+,-_=[-b + or - the square root of (b^2 - 4ac)]/2a = [6 + or - the square root of {-6^2 -(4)(1)(3)]/(2)(1) = (6 + or - the square root of 24)/2 = (6 + or - 2square root of 6)/2 = 3 + or - the square root of 6.](graphics/rationalbasiceqn5.gif)