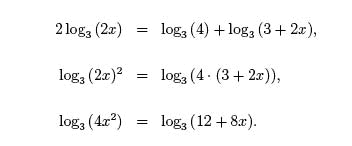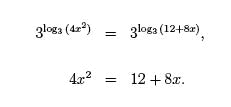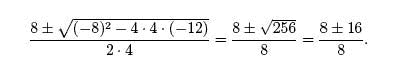In this section, we will learn to solve equations which contain an exponential or
logarithmic function. We will begin by considering two simple equations,
(1) 5ex = 11,
(2) log (2x) = 3.
To solve (1) and (2) we need to find the value(s) of x for which the equations are
a true statement. It is important to realize that (1) and (2) are NOT true for all
values of x. Let’s begin with equation (1).
Solution to Equation 1:
5ex = 11
Just as in solving any other equation, our goal is to isolate the term involving x. Here, we begin by dividing both sides of the equation by 5,
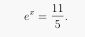
Now that the term ex is by itself on one side, we must “undo” the exponential
to free-up x. Since our exponential has base e, we take the base e logarithm of
both sides (i.e. the natural logarithm of both sides),
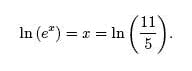
Thus, the solution to equation (1) is
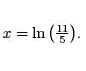
Solution to Equation 2:
log (2x) = 3
In this equation, the term involving x is already isolated to one side of the equation. Therefore,we begin by “undoing” the base 10 logarithmic function by exponentiating both
sides of the equation with base 10,
10log (2x) = 2x = 103 = 1000.
Therefore, we find the solution of equation (2) to be
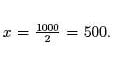
Now we will try
solving some more challenging equations.
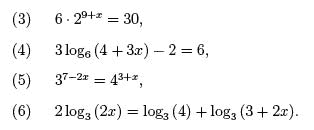
While these equations may look more complicated, our goal is still the same:
solve for the value(s) of x that make the equations true statements.
Solving exponential equations that use bases not found on your calculator
Solution to Equation 3:
6 · 29+x = 30
We begin by isolating the term involving x,
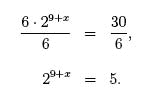
To solve for x, we must undo the exponential. Even though the exponential is
base 2, we will use the common (base 10) logarithm since it will be easier to get
an approximate answer on our calculator,
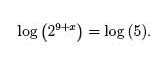
Using properties of logarithms, we simplify the above equation as,
(9 + x) log (2) = log (5).
Solving for x gives,
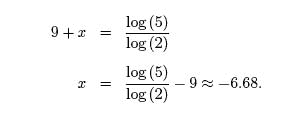

You can always check your answer by substituting the exact answer you found
back into the original equation.
Solution to Equation 4:
3 log6 (4 + 3x) − 2 = 6
We begin by isolating the term involving x,
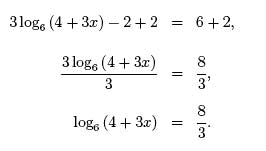
In order to solve for x, we need to free x up from inside the base 6 logarithm.
To do this, we exponentiate both sides with base 6,
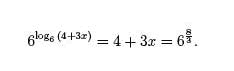
Solving for x we have,
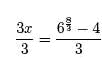
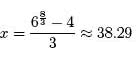
Solving equations that have exponentials with different bases
Solution to Equation 5:
37−2x = 43+x
In this equation, the exponentials have different bases. We will take
the common (base 10) logarithm of both sides to undo these exponentials, and
use properties of logarithms,
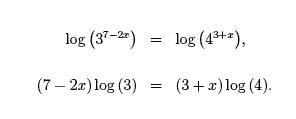
Bringing terms involving x to one side and all other terms to the other,
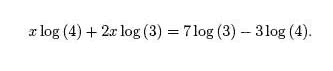
Factoring out x yields,
![x[log(4) + 2log(3)] = 7log(3) - 3 log (4)](graphics/logeqn16.gif)
Now we can solve the equation
![x = [7log(3) - 3log(4)]/[log(4) + 2 log (3)] = 0.985](graphics/logeqn17.gif)
Solving equations with multiple logarithms
Solution to Equation 6:
2 log3 (2x) = log3 (4) + log3 (3 + 2x)
There are two things to notice in this equation: both sides have logarithms, and
one side has multiple logarithms. When dealing with multiple logarithms on a
single side, the easiest thing to do is combine them into a single logarithm using
the
properties of logarithms. In doing this, however, you need to check your solutions
when you are done solving the problem because combining logarithms can produce extraneous solutions.
We begin by simplifying both sides using properties of
logarithms,
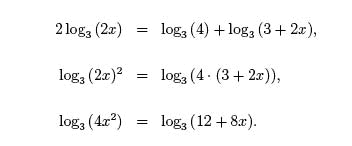
Exponentiating both sides with base 3 gives,
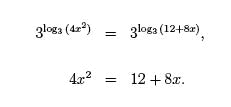
To solve for x, we must solve the quadratic equation,
4x2− 8x − 12 = 0.
Using the quadratic formula, the solutions are given by,
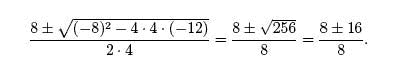
Thus, we find the solutions to be x = 3 and x = −1. Since we combined
logarithms, we must check these solutions in the original equation. Checking
x = 3 gives,
2 log3 (2 · 3) = 2 log3 (6) ≈ 3.26,
on the left hand side and,
log3 (4) + log3 (3 + 2 · 3) = log3 (4) + log3 (9) ≈ 3.26,
on the right hand side. These solutions check.
The solution x = −1 however,
does not check. If we attempted to substitute
x = −1 into the original equation,
we would have,
2 log3 (2 · −1),
on the left hand side. Of course the logarithm of a negative number is undefined
on the real line, and we conclude x = −1 is an extraneous solution.
Therefore,
we conclude the solution to equation (6) is x = 3.
*****
Now try some practice problems using logarithms and solving logarithmic equations.
Problems
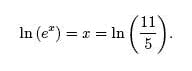
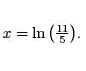
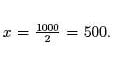
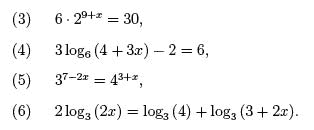
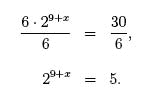
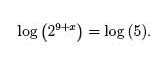
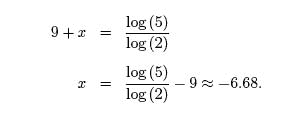

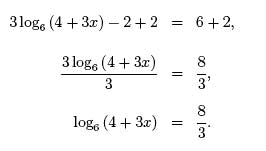
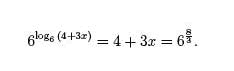
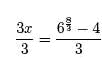
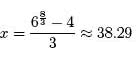
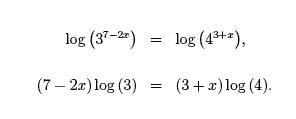
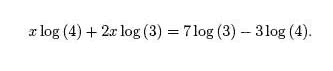
![x[log(4) + 2log(3)] = 7log(3) - 3 log (4)](graphics/logeqn16.gif)
![x = [7log(3) - 3log(4)]/[log(4) + 2 log (3)] = 0.985](graphics/logeqn17.gif)