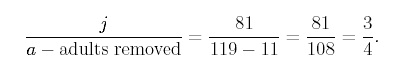Linear Functions
Applications
|
Applications that involve linear equations come up in biological research all the time- from the daily calculations used to make solutions to plotting and analyzing experimental data. Knowing how to model and solve linear equations can also help you find missing information. Here we present just a few applications of linear equations that you might run into during your study of the life sciences. Mixing Acids Consider a solution of 1.00 M hydrochloric acid (HCl), and suppose we add 5.00 M HCl to this solution. If we begin with 565 mL of 1.00 M HCl, we would like to know how many grams of HCl there will be in the solution after x milliliters of 5.00 M HCl have been added. We can use a linear equation to compute the number of grams of HCl in the solution after x mL of 5.00 M HCl are added as, y(x) = mx + b. We first determine the initial mass of HCL in solution, represented by b in the linear equation. To make the conversion we have the following,
where 36.5 g is the formula weight or molar mass of HCl. Now we must compute the
Thus, 0.183 g of HCl are added per mL of 5.00 M HCl. Therefore, the equation given by, y(x) = 0.183 x + 20.6, can be used to compute the number of grams of HCl there are in the solution after x mL of 5.00 M HCl are added. Once y is computed, you can find the molarity of the new solution by computing the number of moles of HCl (from y) and dividing by the number of liters of solution. For example, after adding 5.00 x 102 mL of 5.00 M HCl there are 112 g of HCl in the solution, y(500) = 0.183 · 500 + 20.6 = 112. The new solution will have a molarity of,
What is that number? Our first example showed how linear equations are commonly used in a chemistry mixture problem. A system of two linear equations can also be used in rare instances, such the following situation. Consider an insect species with juvenile and adult stages that is cultured in the laboratory. A laboratory record indicates that there were 200 total insects in the culture at a particular census time, and the experimenter removed 11 adults from the culture so that the juvenile to adult ratio would be 3 : 4. However, someone spilled a solution on the notebook, and where you should see how many of the 200 insects were juveniles and how many were adults, now you see only an inkblot. You want to repeat this experiment under a different set of conditions. Given the limited information provided, how will you find out how many of the 200 insects were juveniles and how many were adults? We can use linear equations to solve this problem. We begin by using the first piece of information given, that there were a total of 200 insects. We will use the variable j to represent juveniles and a to represent adults. We write the following equation, j + a = 200. Since we have two unknowns to solve for (j and a), we need another equation. We now use the fact that 11 adults were removed so that the juvenile to adult ratio would be 3 : 4. We must translate this into mathematics. We know that there are to be 3 juveniles to every 4 adults after the 11 adults are removed. There are different ways we can express a ratio using equations. Using whole numbers, the expression x = 2y means that there are 2 x’s for every 1 y; in other words, the ratio of x to y is 2 : 1. To convince yourself that x = 2y indicates a 2 : 1 ratio of x to y, substitute x = 2 into x = 2y to get y = 1. In the equation x = 2y, the larger number 2 (the smaller number 1) goes in front of y (x) because there are fewer y’s than x’s (more x’s than y’s). In a similar way, we can express the 3 : 4 ratio of juveniles to adults after 11 adults were removed using the following equation, 4j = 3(a − 11). We now solve this system by substitution, substituting j = 200 −a from equation 1 into equation 2 as, 4(200 − a) = 3(a − 11). Solving for the variable a by distributing and combining like terms gives, 800 − 4a = 3a − 33, 833 = 7a. Therefore, we find that a = 119. To find j we substitute a = 119 into either equation as, j = 200 − 119 = 81. Thus, we conclude that out of the 200 insects in the cultures, there were 81 juveniles and 119 adults. It is easy to check that, j + a = 81 + 119 = 200, and,
Now try some problems that use linear functions |
The Biology Project > Biomath > Linear Functions > Applications
The Biology Project
Department
of Biochemistry and Molecular Biophysics
The University of Arizona
January 2006
Contact the Development Team
http://www.biology.arizona.edu
All contents copyright © 2005. All rights reserved.
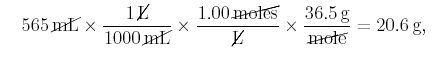
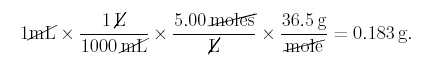
![[112 g (strikethrough)/ (0.5 + 0.565) L] x 1 mole/ 36.5 g (strikethrough) = 2.88 M.](images/linmodeleqn12.gif)