Day 26, MAT115

• Your quiz today will be over distinguishing knots and links: tricolorability and the Reidemeister moves.

• You have a reading assignment over infinity.

  One of my students just discovered this Netflix documentary, A Trip to Infinity; I haven't seen it, but apparently at nine minutes in there's a discussion of Hilbert's Hotel which the student found useful.

• Time for another art contest! Here is the (juried) gallery.

  I'll flash through them, you vote, and some of you will get an extra "get out of quiz free" card.

• Reminder: we're a week and a half from our project and logo demonstrations (the last week of class).

  Don't wait for the last minute! (It usually shows, if you do....:_ )

• We went over the quiz.
• We got started on a really big topic: Infinity....

• We talked about its connection to eternity: what's another ten thousand years when you have an eternity?

• Learned that it's not a number, and tried to figure out a better way to trash talk on the playground.

• Infinity is also not a Size, either, but that's because there is more than one size of infinity! This is the most important thing I want you to remember. (This fact will allow you to win on the playground!;)

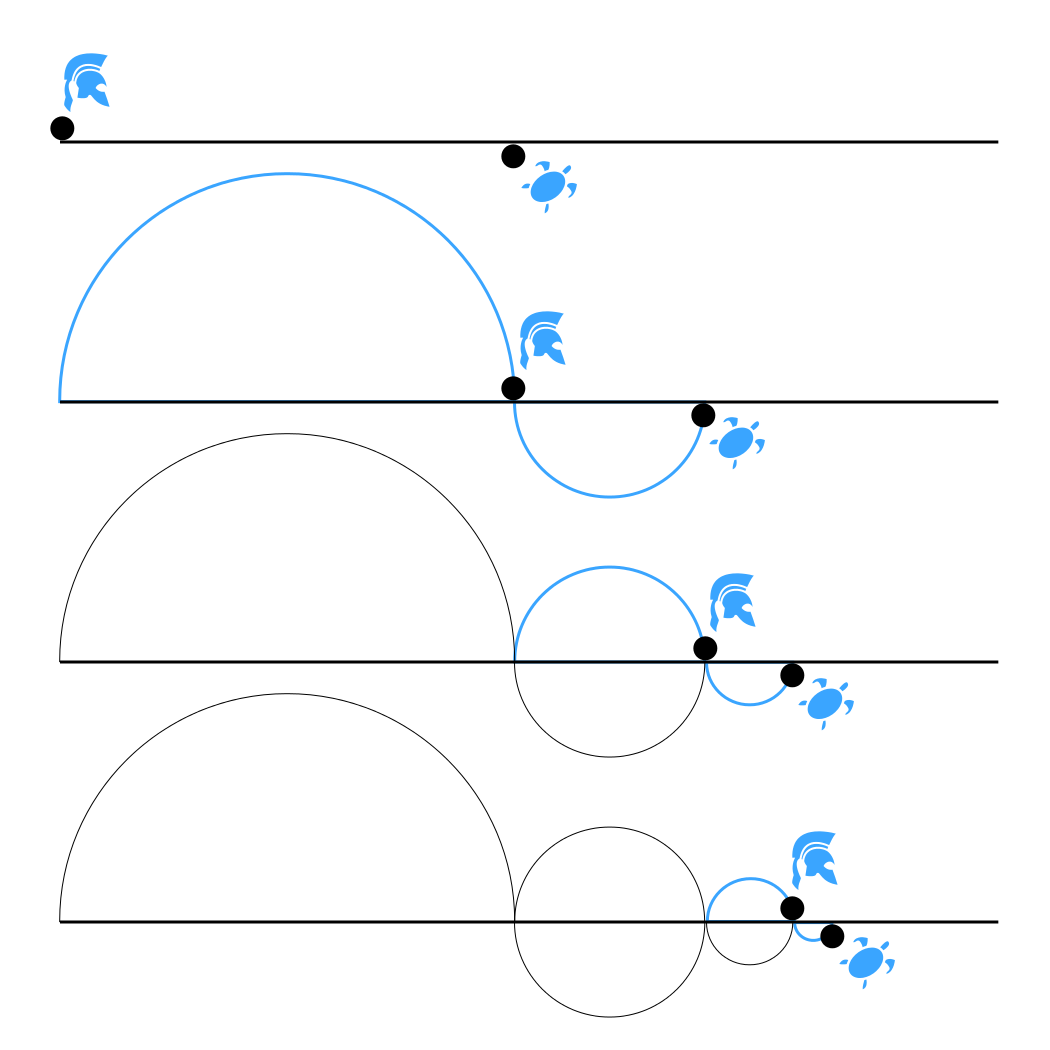
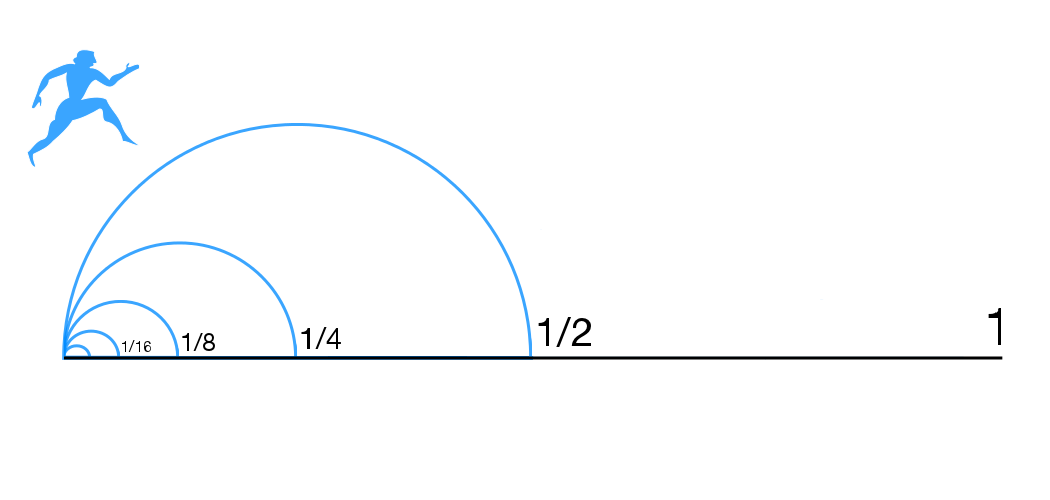
• Examined two of Zeno's paradoxes:
  • Achilles and the Tortoise (the Tortoise beats Achilles.)
    

  • The Dichotomy paradox (Motion is impossible.)
    

• Defined Cardinality It is the way that we describe the size of sets (finite and infinite):

  Two sets have the same cardinality if they can be put into one-to-one correspondence.

  Intuitively: We will say that two sets have the same size if they have the same cardinality.

• Started in on Hilbert's Hotel, and found ways to accomodate
  • One additional guest couple
  • One infinite school bus
  • An infinite number of infinite school buses
  But we couldn't accomodate a real-numbered bus, as we showed with Cantor's diagonization argument.

Question of the day:

• Strap on your seatbelts: are you ready to believe as many as six impossible things before lunch?

• Infinity! A really big idea.... maybe impossibly big. It might even "blow your mind", as it may have for Georg Cantor, the mathematician who introduced us to many of the ideas we talk about today.

• The natural numbers are infinite in number (the size of the set is larger than any natural number). It is called a countable infinity (or denumerable), because, well, we can start counting it! (We just never get to the end -- it will take us an eternity).

• Let's review our results from last time (handout):

  In particular I want to share two other ways to think about dealing with the case of an infinite number of school buses.

  • Last time we assigned bus passengers to unique powers of primes, by bus and seat numbers $(b,s)$:

    $$(b,s)⟶p_b^s$$

    where by $p_b$ we mean the $b^{th}$ prime number. Each person was assigned to a unique prime factorization, meaning no collisions.

    The problem: we don't even know which natural numbers are prime -- there's no rule. We just know that there are infinitely many....

  • Assigning bus passengers to unique powers of 2 and 3: $$(b,s)⟶2^b{3}^s$$

    Now everyone knows exactly where to go! And hopefully the bellhops will get your luggage to the right room, too.

    The problem: the correspondence isn't actually one-to-one -- for example, Room 5 is empty, and feeling lonely at the dance.

    But the Hilbert Hotel (of natural numbers) is certainly big enough to accommodate everyone.

    The little infinity that could!

  • Assigning from a graph
    

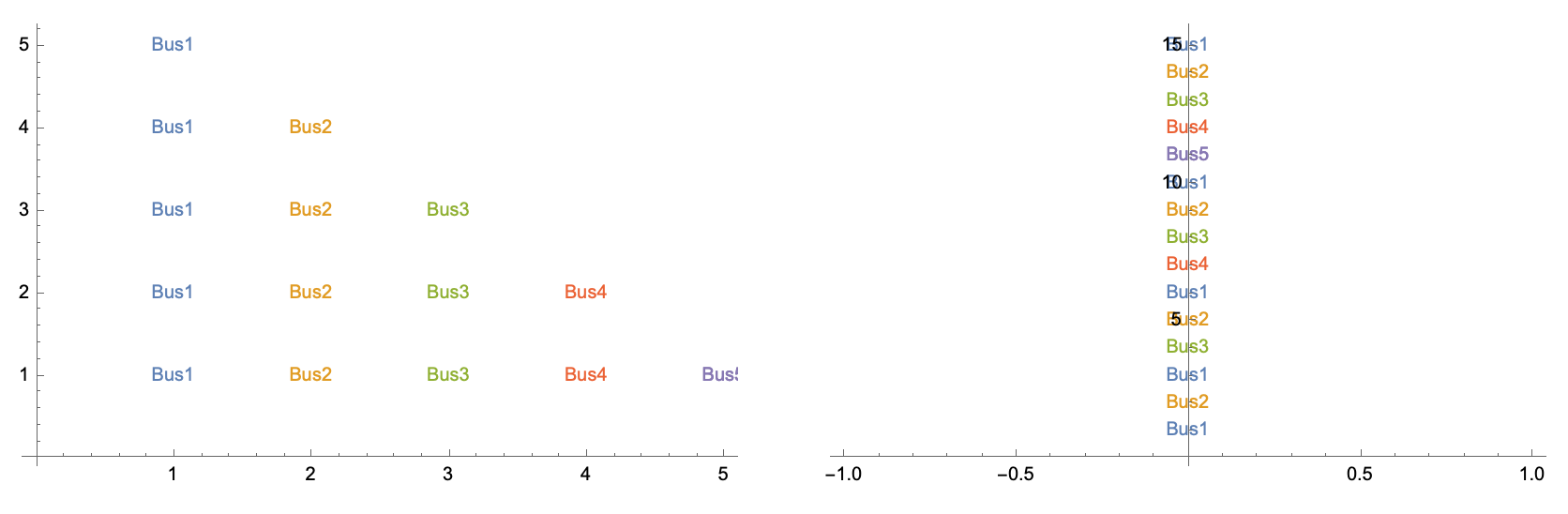
    (for this one, you can see that the two sets are actually in a one-to-one correspondence; for the others, we see that the natural numbers are at least as big as an infinite number of copies of the natural numbers -- but that should seem pretty obvious...!:).

    If I put the people in the Hotel in the first column (we'll call it Bus 1), you can see that they go into the rooms numbered by the triangular numbers: 1, 3, 6, 10, 15, ....

    $$n⟶\frac{n(n+1)}{2}$$ More generally, for the person sitting in seat $s$ on bus $b$, $(b,s)$, $$(b,s)⟶\frac{1}{2}(b^2+b(2s-3)+s^2-s+2)$$ This is a one-to-one correspondence between the natural numbers and infinitely many copies of the natural numbers.

  Looking at it another way, we can see that the rational numbers (ratios of natural numbers, and the negatives of those) are the same size (have the same cardinality) as the natural numbers:

  If we think of a bus/seat pair as a fraction, $(b,s)\equiv \frac{b}{s}$ we see that every positive rational number has its own room within the natural numbers. In fact, they have infinitely many rooms, since, for example, $$\frac{1}{1}=\frac{2}{2}=\frac{3}{3}=\frac{4}{4}=\dots$$ all get rooms (but they're the same rational number!).

• Here's the upshot of what Cantor discovered:
  1. Some mathematical facts:

     Mathematical fact zero:

     A set S is just a collection of objects; and a subset of S is just what you'd expect: some members of S. It may be all the members, in which we call it an "improper" subset, or it may be none of them (in which case we call it the empty set).

     We often denote a set by using braces, e.g. $S=\{1,2,3\}$ is the set of the first three natural numbers.

     We say that $a$ is an element of $S$ if $a$ is contained in $S$, and we write $a\in S$. So $1\in S$, $2\in S$, and $3\in S$. We deny that an object is in $S$ this way: $4\notin S$.

     Mathematical fact one:

     A subset is never bigger in size than the set itself.

     And if the sets are finite, the proper subset is always smaller, but if the set is infinite, we may actually be able to throw away elements of a set and not change the size of the set!

     Mathematical fact two:

     Let's call the set of all of a set S's subsets its power set, $P(S)$. Pascal's triangle (that rascal!) shows you how many of each type of subset you have (for finite sets).

     1 3 3 1

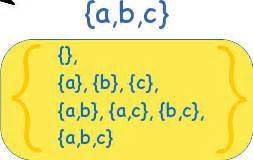
     Mathematical fact three:

     The power set of a set of $n$ elements contains $2^n$ elements.

     (We know that since each row of Pascal's triangle adds to a power of 2.)

  2. Even the set containing no elements has one subset -- the set itself. So the power set has one element -- has size bigger than the set itself.

     This property holds true for all finite sets -- and it turns out to be true for infinite sets, too!

     Here's a silly video to illustrate how the power set grows with sets of increasing size. (Thanks to Dr. Towanna Roller (Asbury University) and her daughter Kristyn Roller (UK) for this one!)

  3. This means that, although the natural numbers $1,2,3,\dots$ is infinite as a set, there's a bigger set (the power set of the natural numbers).

     And the power set of that set is bigger yet, and so on forever, forever, Hallelujah, Hallelujah!

  4. And the power set of the natural numbers is a set, having a power set of its own: $P(P(N))$. And that power set is bigger yet, and so on, and on and on, and on, and on, and on,....

  5. Upshot: infinity comes in various sizes! Infinitely many, in fact. Crazy sounding, I know -- but it's true.

     That symbol that you've been familiar with for all your lives, $\mathrm{\infty }$: you thought it stood for a single thing; but it stands for a whole collection of monstrously big things, all too big to really think about properly. (Well, Cantor did!:)

  6. That's too crazy, it seems; but, nonetheless, mathematicians know that it's true, because we can prove it! The key to determining if two sets have the same size is the one-to-one correspondence -- and that is key for infinite sets, as well.

  7. So, in the end, here's what you say on the playground, when you want to love your friend more:

     "I love you more than the power set of your set of infinite love."

     

     Amen!