Day 23, MAT115

• This week's quiz will be over bands, knots, and links: recognition, drawing, etc.

  You may bring your own knots to the quiz.

• Lexi has home softball games on the following days/times:
  • Tuesday, April 2, 2:30 -- that's today! Given the rain, maybe not....
  • Saturday/Sunday, April 13/14, TBD?
  • Wednesday, April 24th, 2:30
  • Friday, April 26th, 3:45

• Anyone else have events upcoming that we should know about? Theater? Music? Please send them to me, and I'll add to the announcements.

• Slight change in schedule: I want to spend a couple of more days with Knots and Links, learning to distinguish them. Then we'll hit Infinity, and follow that with Angels and Miracles. Here's infinity as an unknot:
  

• You have a new assignment, about the material we are discussing today.

  Some reading, and try to tricolor some knots.

• You had a homework that was to be a small part of the exam: to make some pretty knots, and take a picture, and send to me.

  Some of you evidently didn't realize it, and so have not submitted that. If you would like to, submit it by Thursday.

  Then we'll have another art contest. But we have an early "judge's choice" winner: Mae's knot pretzels. Here they are,

  • going into the oven, and
  • hot knots!

• We had an exam! Let's talk about that.
  • I enjoyed digging up the local logos, and finding out which ones have some interesting mathematics in them. I found too many to include them all: for example, the Duke Energy logo is a Hopf link (if the bands weren't cut...:)
    

  • Key

  • I found out that wallpapers were tricky, and I decided to handle the scoring of your exams to minimize the damage. So you have two scores at the top of your exam: the score for the first four pages of your exam, and the score on the last problem (the wallpaper problem). (There is also the five-point knot picture points, depending on whether you submitted your knot picture or knot -- I haven't included that part).

    Now, if

    • your wallpaper score was a better percentage than your score on the first portion, it got included into your score (which will then be out of 100);
    • it was worse than the first part, it got dropped, and your score will be the percentage on the first part (out of 80, where your knot picture score will be included).
    So the wallpapers can help, but not hurt.

    They were tricky!

    On this problem I ended up just looking for good reasoning: Both of these wallpapers actually have $R_2$ symmetry, and the one on the left has two lines of reflection (whereas the one on the right has none).

    Then we look into the types of centers of rotations....

    1. It's an interesting fact about prime decomposition of numbers that tells us that the one on the left has order of rotational symmetry $R_2$:

       while hexagons (with their 6 sides) suggest that an $R_6$ is possible, the inside "flower" has 16 petals. In order for both of these patterns to fall back on themselves, the rotation must be a common divisor of 6 and 16. The ONLY common divisor of both is 2: $6=2\ast 3$ and $16=2\ast 2\ast 2$.

       The wallpaper also has two perpendicular lines of reflection.

       In the end, that drives us to conclude that this is $D_{2_{kgkg}}$.

    2. The other pattern is also $R_2$, and has no lines of symmetry. There are therefore only two patterns to choose from, $C_2$ and $D_{2_{gggg}}$.

       But our pattern only has symmetry about two centers, whereas $C_2$ has three. Thus, by deduction, we've discovered the pattern for this wallpaper, and it's $D_{2_{gggg}}$.

How do we distinguish knots?

• Before we get to that, however, I want to introduce you to the "RCO" -- Really Cool Object -- which brings together the Borromean rings, golden rectangles, and Platonic solids (an icosahedron).

  This is the most beautiful piece of mathematics I know:

  It turns out that there are golden rectangles in the heart of an icosahedron, interlocked as Borromean rings!

  

  We'll make some using 3x5 (or 4x6) cards -- which are not quite golden. Their corners are the 12 vertices of the icosahedron. The tricky part is locking them together!

• A little review, and a preview of what's ahead: trying to distinguish this collection of knots (and links, too!).
  • The figure-eight knot has four crossings, as does Solomon's "knot" -- but Solomon's "knot" a link, not a knot. This is the first (interesting) instance of a knot and link with the same (minimal) number of crossings.

    But we can easily figure out which is which, because the knot is a single continuous piece of material, whereas the link is two separate pieces of material.

  • We know that there are two distinct 5-crossing knots (we can see them in Rolfsen Knot Table)
    • The cinquefoil knot
    • The five-crossing twist knot is actually known (somewhat confusingly) as the 3-twist knot

  • How can we tell them apart? Are they really different? For that we need to study knot equivalence, and our primary tool, the Reidemeister moves.

• How do we show that two knot projections ("squiggles") are the same knot ("knot equivalence")? That's the job of the Reidemeister moves.
  1. What are the Reidemeister moves?
     • Tools for showing that two projections (pictures) of knots really show the same knot.
     • Names of the moves reflect the number of strands involved. A Strand is a piece of a knot picture that goes from undercrossing to undercrossing, with only overcrossings inbetween.

       It's all about overs and unders!

     • Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.

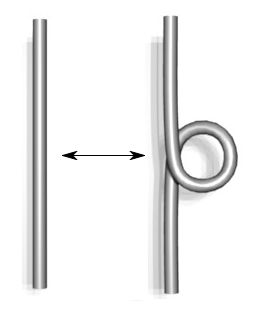
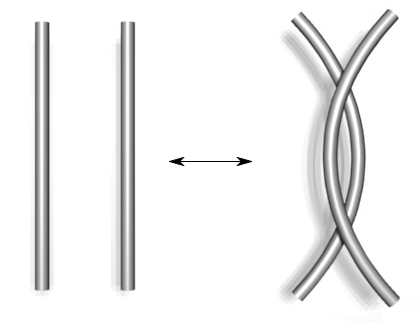
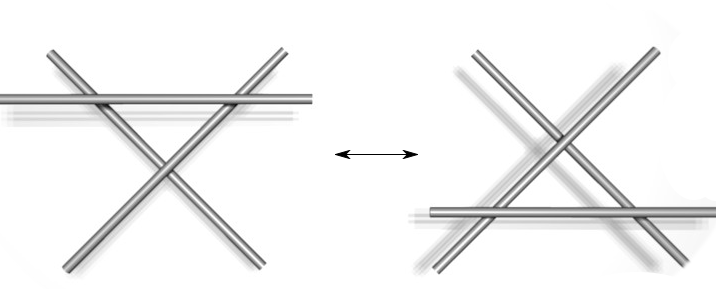
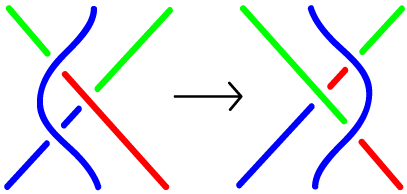
     • Type I	Type II	Type III

  2. Here's a summary of the moves.

     The third images on that page stems from this picture from a recent Science issue:

     In order to consider the picture on the left a knot, we have to know what its ends are doing. In the figure at right, I assumed that they are just connecting to each other in the simplest way.

     The succession of steps then go on to show that the knot is actually an unknot! That's good news for the hypebusy people!

  3. Using the Reidemeister moves
     1. to turn a projection of an unknot into another more complicated appearing unknot:

        Here's another picture of an unknot, which could trick you -- but knowing the R1 move saves you:

        

        We'll just try a few with a string, to see what we can learn.

     2. Now let's use these three moves to create equivalent versions of the trefoil knot, but using each of the three Reidemeister moves.

     3. A figure-eight knot is equivalent to its mirror reflection (a trefoil knot is not equivalent to its mirror!)

     4. Turning a more complicated appearing unknot into a simple circle unknot. (Here it is as a powerpoint presentation.)

  4. Reidemeister moves and Tricolorability
     1. Tricolorability: "A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:
        1. At least two colors must be used,
        2. at most three colors are used, and
        3. at each crossing, the three incident strands are either all the same color or all different colors.

     2. Tricolorability is preserved by Reidemeister moves:

        Reidemeister Move I is tricolorable.	Reidemeister Move II is tricolorable.	Reidemeister Move III is tricolorable.

     3. Therefore, if the projection of one knot is tricolorable and the other isn't, they're different knots (because we can't get from one to the other via Reidemeister moves).

     4. Theorem: there are at least two different knots.
        1. The unknot is not tricolorable ("At least two colors must be used");
        2. The trefoil knot is tricolorable:

        3. The figure-eight knot is not tricolorable (it requires four colors):
        4. Danger: be careful what you conclude:
           • Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)

           • many knots are tricolorable -- in fact, infinitely many! -- so being tricolorable doesn't mean that your knot is the trefoil knot -- but it does mean that your knot is not the unknot, for example.

             So, for example: if you've got your picture of a knot down to three crossings, and it's not tricolorable, then it's the unknot.

           • And among knots and links with five crossings or fewer, only the trefoil and the unlink are tricolorable.

• 17 Wallpaper Groups: how to distinguish them.
• Some Solid (Three-dimensional) Geometrical Facts about the Golden Section