- Apologies to those who came on Friday -- I was terribly late, and
missed at least one student.
I'll try my hardest to do better this coming Friday.
- There is a new assignment in IMath, on chain rule
problems. You have several open at the moment. Please keep up
with those.
- There will be a public lecture next Wednesday evening entitled
Covering Climate by Peter Prengaman, who is the Climate and Environmental news director for the Associated Press. - I'm pleased to announce that we will be hosting Mr. Prengaman on
Wednesday (as well as Mark Neikirk, of the Scripps Howard
Center for Civic Engagement here at NKU). So class will be a
little different.
Here's my plan (although I'll be discussing with Mr. Prengaman at dinner on Tuesday night):
- Please sit near front-n-center for Wednesday's class.
- I'll make a short presentation about some climate change issues
- We'll examine several mathematical models to acccount for the the early blooming of the Cherry blossoms in our nation's capital. (This example is inspired by a recent article in the climate press.)
- Then I'll turn things over to Mr. Prengaman, to lead a discussion. But all good discussions require participation!:)
- Your presence on Wednesday is your quiz grade. Actually, you
will have a 7.5/10 by your presence. If you are engaged, you
will receive a higher grade; if you're on your phone, you'll
receive a lower grade.... Participate to assure that you get a
10!
- Your elementary derivative rule quiz:
- My kid long ago purchased a board game: "Following directions". I always liked that name (and the game, actually): not sure that it made him any better about following directions, but...:)
- quiz key
- Then let's talk about some more practical issues:
- factoring when possible
- You've got to know your basic rules (product, quotient, exponential, etc.). A few of you were using the "obvious" (but incorrect) forms of the product rule and quotient rule; one or two of you used the power rule on an exponential
- in conjunction with talking about the chain rule, we
were talking about a sample problem involving compositions: model the
seasonal variation in Keeling's CO2 data.
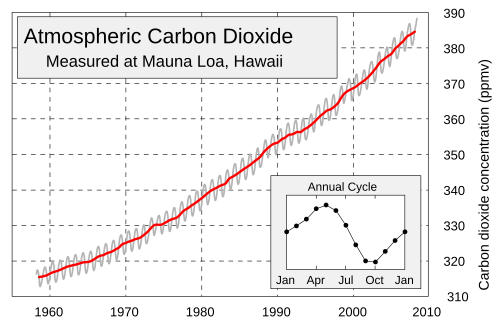
If time \(t\) were measured in years from January first, would
$V(t)=A\sin(2\pi{t})$ be a good model for the data shown in the inset? What would be a good choice for the parameter $A$?
- I distributed a worksheet last time, but
we didn't have any time in class to work on it!
Let's take about fifteen minutes to compare your answers with a neighbor, and then we'll discuss your solutions.
We'll approach this topic via some examples, such as the ones given in the section intro, and in the section preview.
- Consider the relationship between x and y given by
$y(x) = \frac{1}{x}$ We know how to differentiate y(x) with respect to x, using the power rule.
But there's another way to think about this relationship, and that's
$x y =1$ This gives no priority to either variable -- it's symmetric in both.
(This means that the graph of $y$ is symmetric about the line $x=y$ -- and that could be used to find the derivative of $y$ from the derivative of $x$.)
We can still differentiate to find y'(x), however, using the product rule and something called "implicit differentiation". We consider $y$ and unknown (implicitly defined) function of $x$, treating it as $y(x)$; then, since both sides of the equation
$x y(x) =1$ are equal, the derivatives of both sides must be equal. We differentiate both sides, and equate them (using the product rule on the left). From this we obtain the correct derivative, as well.
The solution curves are hyperbolas (one of the "conic sections": those curves you get by slicing a cone).
- Probably the most important example for us to think about is a
circle:
Graph of $x^2 + y^2 = 16\text{.}$One of the issues is that this is not the graph of a function -- it fails the vertical line test. But it is clearly a really important graph for us to be able to do calculus on (e.g. make tangent lines).
One approach to dealing with this object is to divide it into two separate functions: an upper and a lower function, which would look like this: \[ y=\pm \sqrt{16-x^2} \] The upper function corresponds to the "+" sign, whereas the lower corresponds to the "-" sign. But what a pain! This is where dealing with it as an implicit function helps us.
As an example of a problem one might want to solve for the graph above, what are the values of $a$ and $b$ such that the tangent to the circle goes through the point (4,2)?
I can think of two ways to solve this:
- Using geometry and symmetry (and just one equation); or
- Using two equations: the equation of the circle, and the equation of the tangent line.
- Another example is the folium of Descartes, which is the graph
(solution) of the implicit equation
but\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the
solution curve must be symmetric about the line $\displaystyle y=x$:
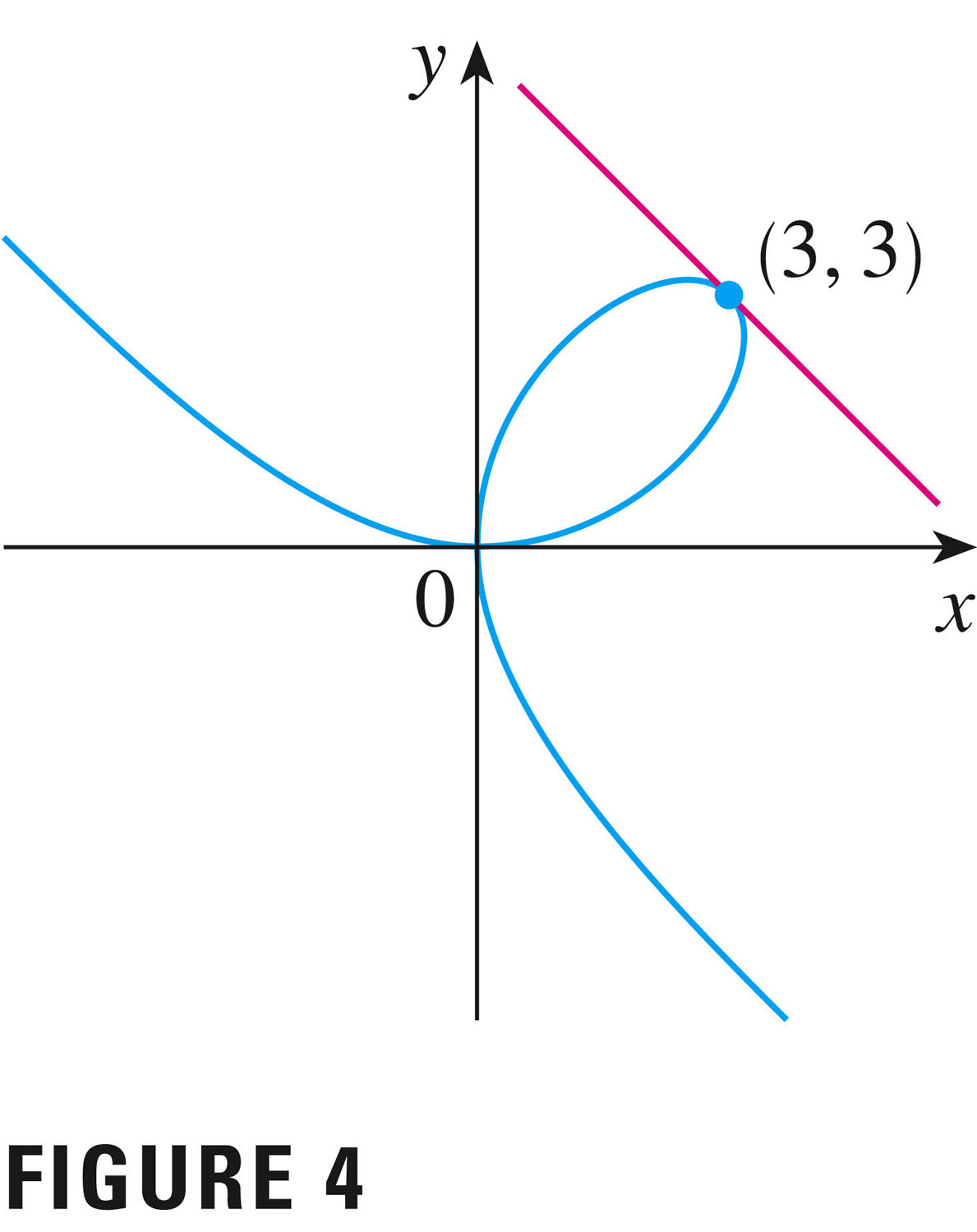
Q: What is the equation of the tangent line shown?
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0))
Q: What are the two equations of the tangent line to the point (0,0)?
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ 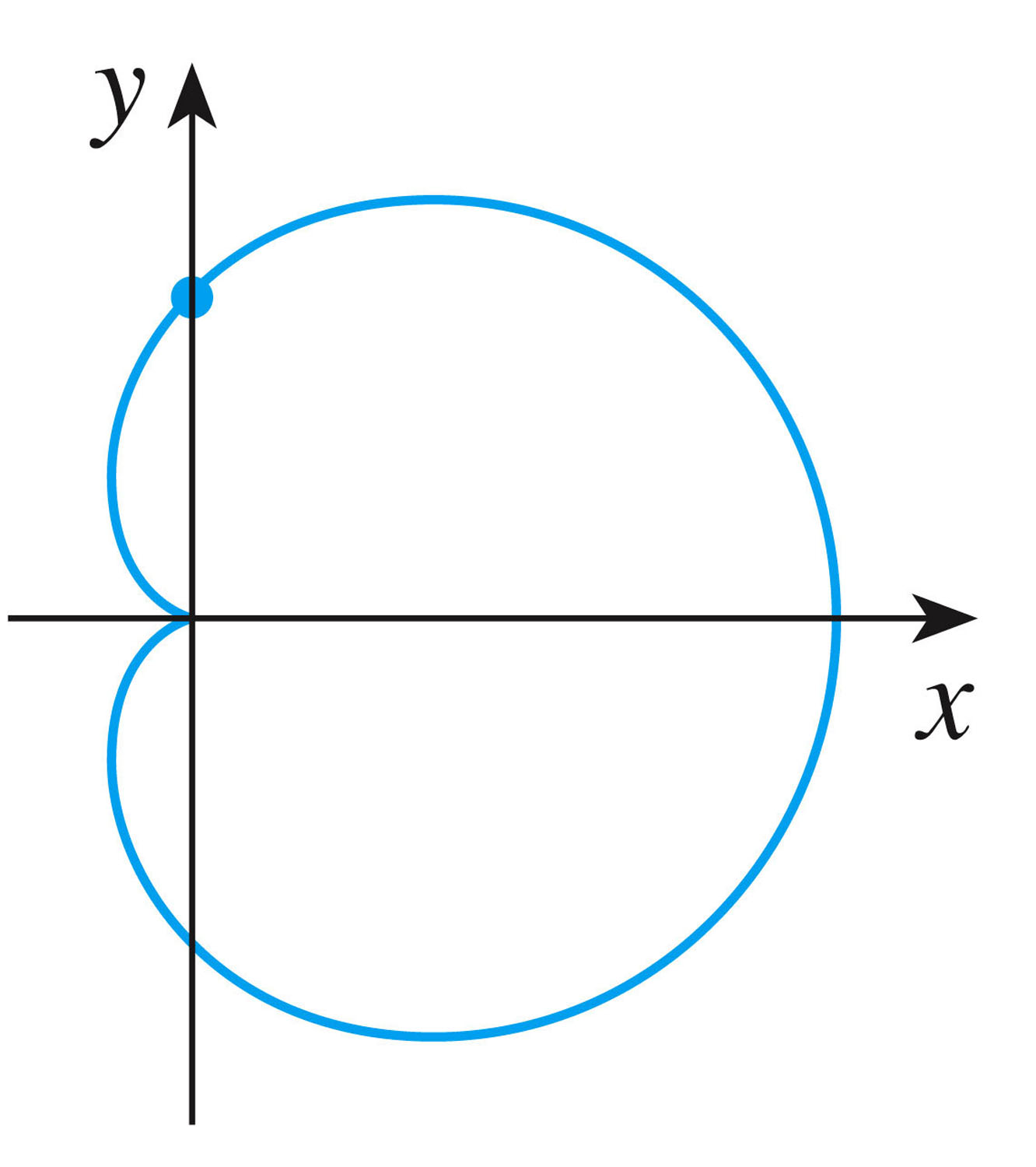
Because the equation is symmetric in $y$ (it's even in $y$), we expect the curve to be a reflection about the $x$-axis (as we can see in the figure).
So if $(x,y)$ is a point on the graph, then $(x,-y)$ will also be on the graph (and vice versa).
$x^2+y^2=x^2+(-y)^2=(2x^2+2(-y)^2-x)^2=(2x^2+2y^2-x)^2$ - Here's a worksheet for us to work on (it includes a few chain rule problems, too: from now on we'll be bumping into more compositions, and compositions shout "chain rule!").
