Today:
- Announcements
- Mat128 has been added to your Blackboard courses. That is an assessment, which
- will be available today, evidently;
- will count as two homework assignment GOHF cards, if you
do it (and all I'll know is whether you did it or not);
- will not affect your grade otherwise. Do your best, that's
all I'd ask: take it seriously.
- Your 5.2 homework may be turned in at the time of your final, and
will count as a homework replacement for a lower one.
- For the final you may have a one-page cheat sheet.
- In this, our final week:
- Today: review of all material
- Sunday night, 7:00-9:00p.m.: review, here.
- Monday: I'll be in from about 8:00 through exam time.
- Last time we began reviewing new material:
- Section 4.3: the Fundamental Theorem of Calculus
- Section 4.4: Indefinite integrals
- Section 4.5: Substitution
- Section 5.1: Areas between curves
- Section 5.2/5.3: volumes (by cross-section and cylindrical shells)
- "Other applications"
I thought that I'd pull a few problems off of my old final(s), to show you some
of the things that I asked:
- Find $\int_0^1 \frac{x}{\sqrt{4-x^2}} dx$, without recourse to
the calculator. In other words, show all steps.
- Now, using your calculator, approximate $\int_0^1
\frac{x}{\sqrt{4-x^2}} dx$ using $R_{2}$, $L_{2}$, $M_{2}$, $T_{2}$ and
$S_{2}$.
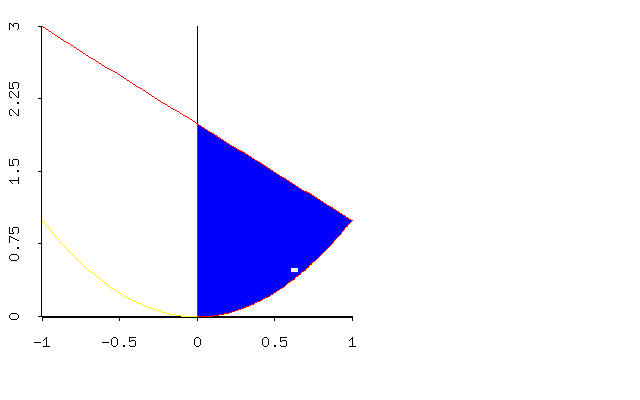
- Consider the positive region bounded by the y-axis, the
function $x^2$, and the function $2-x$, as seen in the following
figure. Compute the volume of the object obtained by rotating this
region about the y-axis, in two different ways: using cylindrical
shells and using disks/rings.
- A population of a large city is radially symmetric about the city
center. Its population density can be modelled well with the density
function $\rho(r)=\frac{1}{r^2+1}$, in units of millions
of people per square mile, and where $r$ is the distance from the
center. Compute the total population within the area 10 miles from the
city center.
- For the function $f(x) = \sqrt{x}+3x^2-\cos(x)$
- Find all anti-derivatives of $f$.
- Find the particular anti-derivative whose value at $x=0$ is 2.
- For the following integrals, indicate the substitutions you would use to
compute the integrals, and rewrite the integral using the substitution (if
necessary - that is, if the integral is not obvious or undefined). No need to
evaluate the integrals.
- $\displaystyle \int_{-3}^{3} x \sin(x^2)dx$
- $\displaystyle \int \cos(x) \sin^3(x)dx$
- $\displaystyle \int_{-4}^{-1} \frac{x}{\sin(x^2)}dx$
- $\displaystyle \int_{}^{} \frac{x-1}{\sqrt{(x^2-2x-5)}}dx$
- Compute the derivatives (with respect to $\displaystyle x$) of the following functions:
-
$\displaystyle \int_{x}^{1}t^2\sin(t)dt$
-
$\displaystyle \int_{1}^{x^2}\frac{t}{5t-3}dt$
-
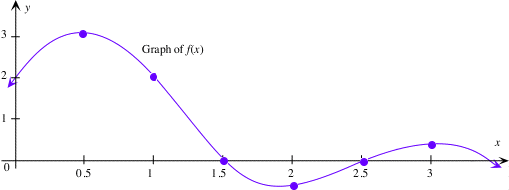
Let $\displaystyle f(t)$ be given by the following graph. Draw a reasonable
graph of $\displaystyle g(x)=\int_{0}^{x}f(t)dt$ on the same axis:
- Draw the region bounded by the two curves $y=20-x^2$ and
$y=x^2-12$, then find the area of the bounded region.
- Today I want to focus on old material.
Website maintained by Andy Long.
Comments appreciated.
