- Your 4.4 homework is returned: graded .
- Your 4.5 homework is due today.
- Your exam revisions are also due today.
Last time we started Section 5.1: the area between curves
There's no great shakes here: we continue to think of integrals as representing areas. In our introduction to the integral, we've begun by thinking of a definite integral as representing a signed area, between a curve and the x-axis. Now suppose that we want the area between two curves:
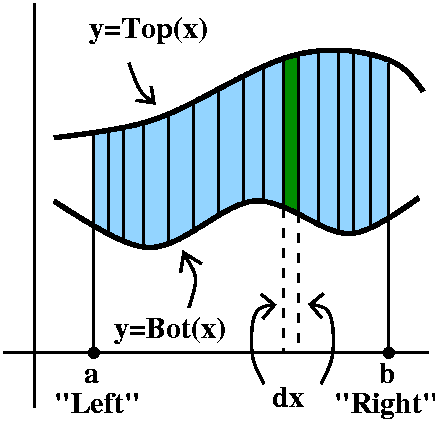
If one curve is always above the other, then we simply subtract the smaller area from the larger:

If the top curve is the graph of $f(x)$, and the bottom curve is the graph of $g(x)$, then the difference in the areas, which is what we want (in blue), is
Let's do some examples.
There are a couple of tricks here:
- One is to figure out what to do when two curves cross:
In this case, the sign of the area changes as
and
change roles (which one is above, which below). If we want the actual geometric area, and not the signed area, then we can use this formula:
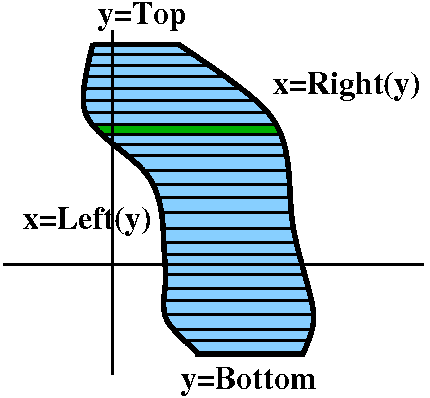
$I = \int_{a}^{b}\left|f(x)-g(x)\right|dx$ - The other trick is integrating along the y-axis, rather than
along the x-axis.
- #2, p. 349
- #3
- #6
- #17 (switch roles!)
- #31
- #41
- #45
- #46
Let's see how to compute volumes of some simple objects using integrals.
Before you may have memorized some of these formulas. Now you can derive them! This is the power of calculus.
In every case for what follows, we begin with what I consider the most important formula for integral calculus:
To calculate any quantity $V$, we simply divide it up into infinitesimal quantities $dV$, and add an infinity of them up.
Now for volumes we usually know the extent of the object, so we'll march along the x-axis from a to b, stop at x, and add in the little $dV(x)$ that is found there. So in each case what we need to do is find $dV(x)$
- The cube of side length $s$:
$dV(x)=A(x)dx=s^2dx$ $V=\int_{0}^{s}dV(x)$ - The right circular cylinder of radius $r$ and height $h$:
$dV(x)=A(x)dx=\pi{r}^2dx$ $V=\int_{0}^{h}dV(x)$ - The cone of radius $r$ and height $h$:
$dV(x)=A(x)dx=\pi\left(r(1-\frac{x}{h})\right)^2dx=\pi{r^2}(1-\frac{2x}{h}+\frac{x^2}{h^2})dx$ $V=\int_{0}^{h}dV(x)$ - The pyramid of height $h$, and base $s$:
$dV(x)=A(x)dx=\left(s-sx/h\right)^2dx=s(1-\frac{2x}{h}+\frac{x^2}{h^2})dx$ $V=\int_{0}^{h}dV(x)$ - The sphere of radius $r$:
$dV(x)=A(x)dx=\pi\left(\sqrt{r^2-x^2}\right)^2dx=\pi(r^2-x^2)dx$ $V=2\int_{0}^{r}dV(x)$ (the "2" is out in front because we're using symmetry: we calculate the volume of half the sphere in running from 0 to r, then double it).
- Examples:
- #48, p. 361
- #52
- #4 and 5, p. 360