Day 9, Mat129: Calculus I

1. Folks, it's the most important definition in calculus. This is calculus class. Memorize it:
   $f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$

2. It's about limits. So should your answer be....

   The limit of a quotient is the quotient of the limits, provided the limits of numerator and denominator exist, and that the denominator $g(x)$ satisfies

   $\lim_{x\to a}g(x)\ne 0$

   For example, here's the graph of $h(x)=\frac{1-cos(x)}{x^2}$ (although there should be a hole at (0,1/2)):

   For this plot, $f(x)=1-cos(x)$, and $g(x)=x^2$, and as $x\to 0$, $\frac{f(x)}{g(x)}\to 1/2$. However it's not the value of $g(0)$ that's the problem: we could define $g(0)=1$ and the limit of the quotient would still exist, and still be 1/2.

3. Continuity is about limits, too. So should your answer be! Three things must happen:
   $\lim_{x\to a}f(x)=f(a)$

1. We saw the importance of both continuous functions, and discontinuous functions.
   • A continuous function carried the signal (e.g. starting from a middle A, of frequency 440, and decreasing by octaves):

   • This picture illustrates the doppler effect (that a train whistle changes frequency as the engine passes you by).

2. Then we multiply that by some other function, to modulate the amplitude or frequency, say -- and that function may be discontinuous:

   Amplitude Modulation:
   Frequency Modulation:

Secant line slopes thus represent an approximation to the slope of the tangent line: we think of them as an "average change" over an interval, whereas the tangent line is the "change" over a point (whatever that means! Actually it means "in the limit...").

The secant line slopes represent an average rate of change of a function, whereas the tangent line slopes represent an instantaneous rate of change of the function.

But it's all about slopes! That's made clear by the important equations on p. 104 and 105.

So our focus is on tangent lines (places where a line osculates a curve):

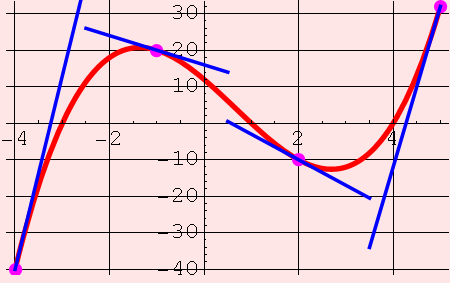
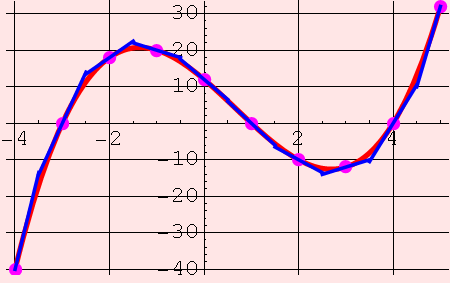
Instantaneous rates of change (slopes of tangent lines)	can be approximated using data. Let's try! We also note that the function can be approximated well by snippets of tangent lines.

Each of the slopes above represent "rates of change" of the function f. What does that mean? The thing that tells you how fast a function is changing is its slope, isn't it? If a function is constant, then it's not changing at all. If the slope is steep (either up or down), then the function's values are changing dramatically and quickly.

The rate of change is dictated by the slope. So it should come as no surprise that the derivative of a function at a point is the same as the slope of the tangent line at a point.

We can approximate tangent lines with secant lines: let's do a little exercise about that now.

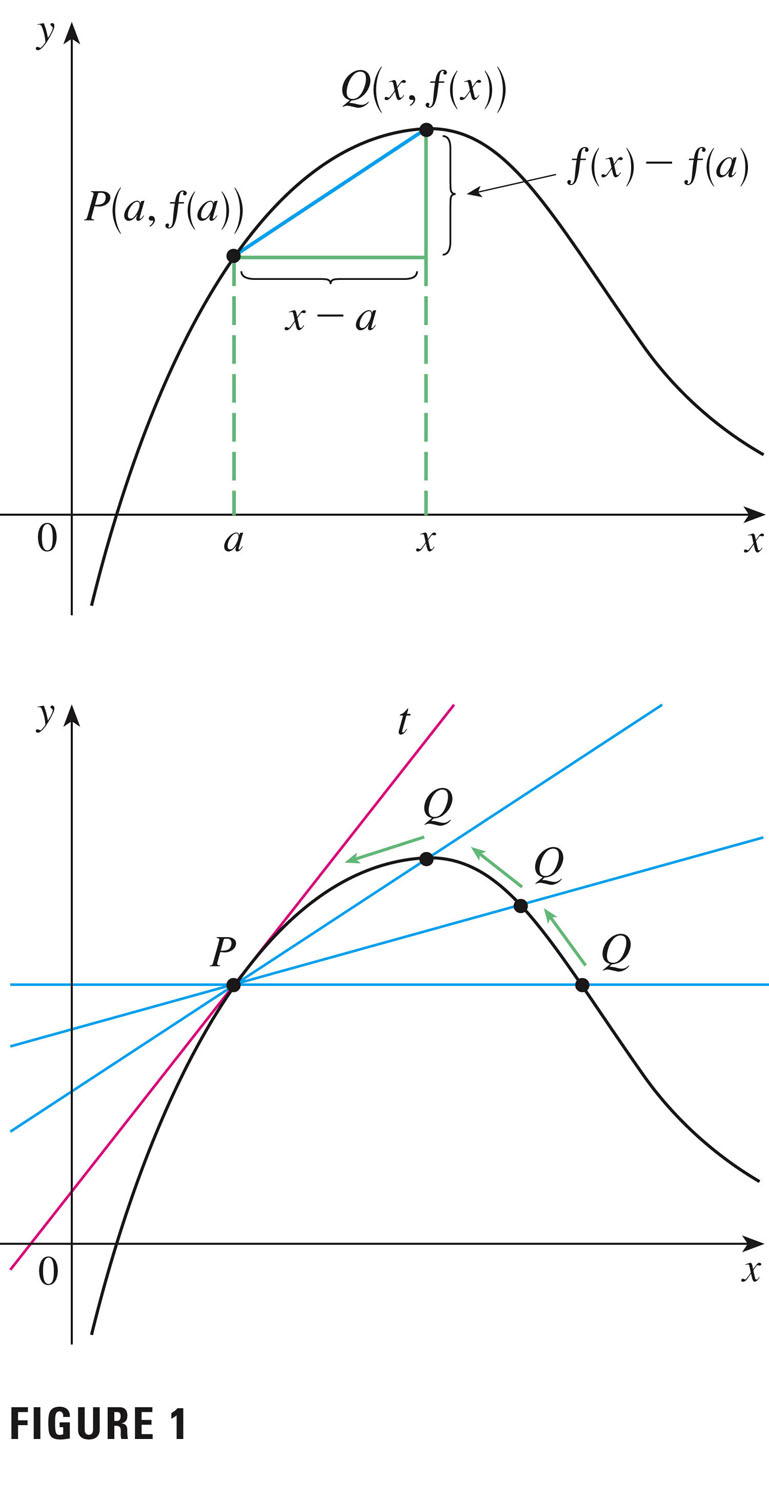
The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment (the slope of a secant line), $\frac{f(x)-f(a)}{x-a}$ This is an average rate of change in f over a finite interval. In the limit, this average rate of change becomes an instantaneous rate of change: $m=\lim_{x\to{a}}\frac{f(x)-f(a)}{x-a}$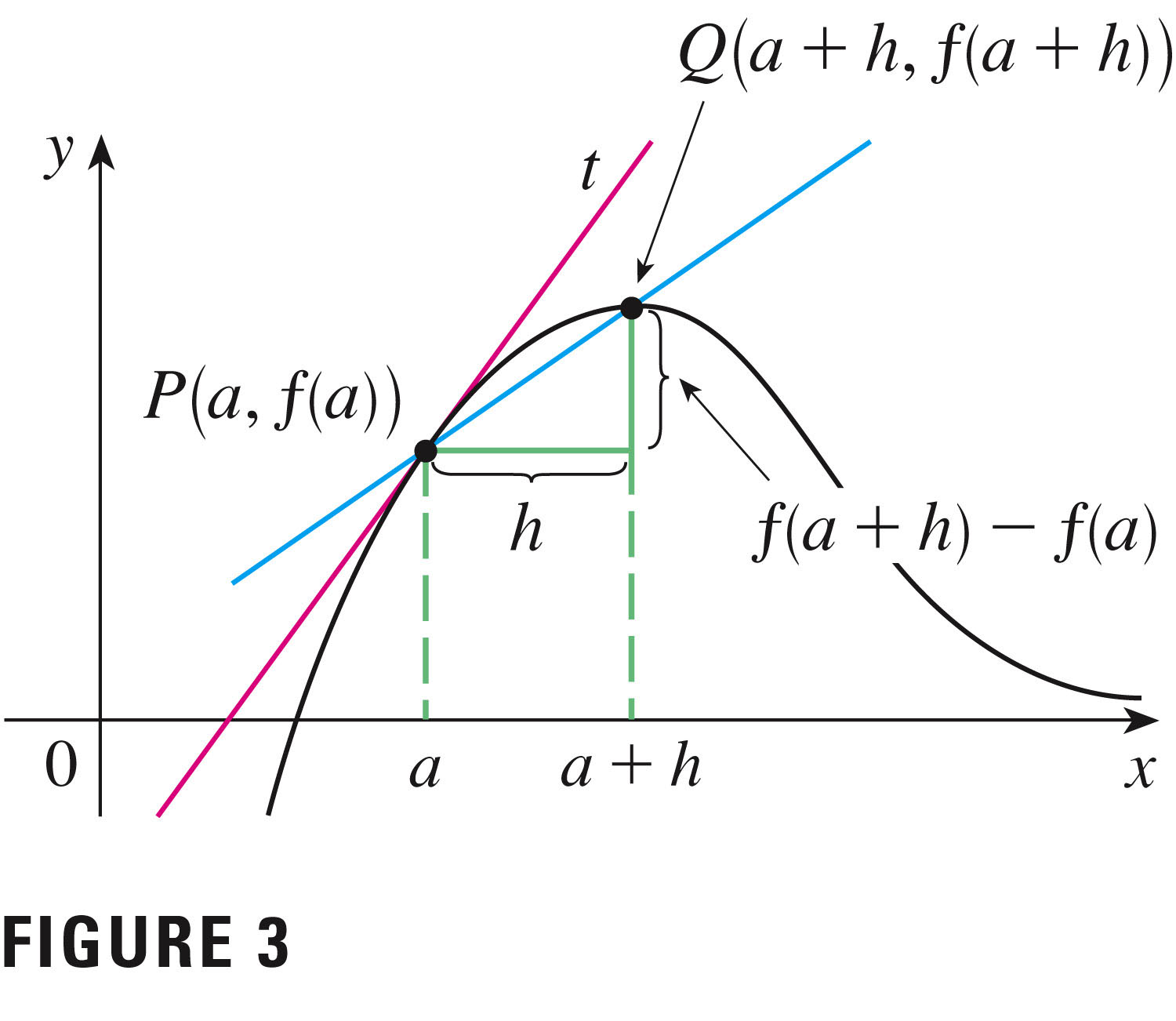

Here's an alternative notation for the slope: The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment, $\frac{f(a+h)-f(a)}{h}$ In the limit, this is $m=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ which I call the most important definition in calculus.

$f^\prime(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}$

The most important definition in calculus! (I just can't say it enough!)

Now let's look at some problems, and see how this concept is connected to real-world problems.

• #3, pp. 110 (two equivalent definitions)
• #11, pp. 111
• #13, pp. 111
• #45, pp. 112
• #51, pp. 113

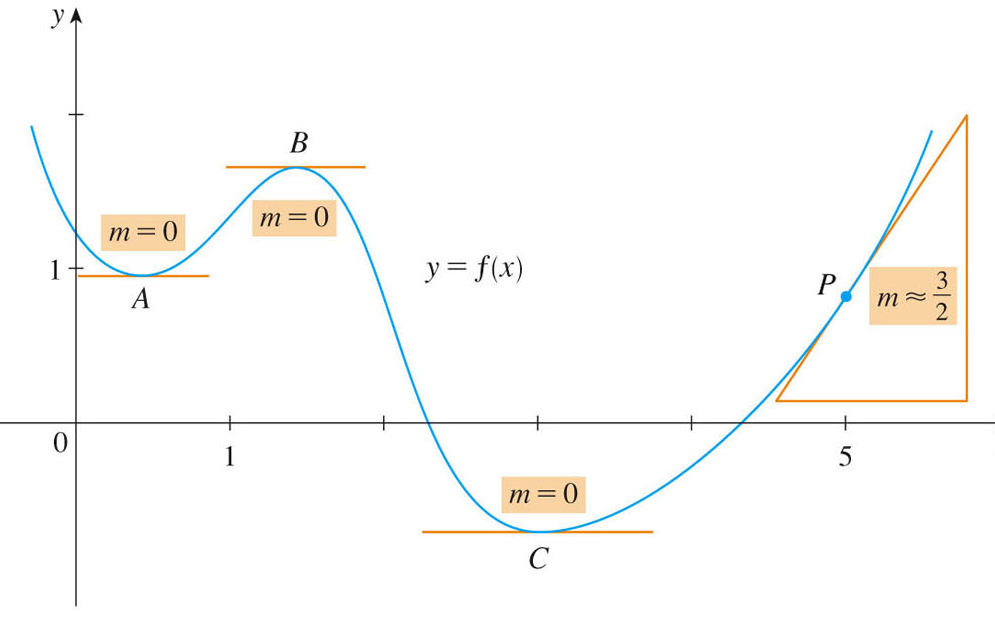
We see the derivative (thought of as a slope) at four separate points (A, B, C, and P). At three of these points we see that the slope (and hence the derivative) is zero. These are especially important points, since, as you can see, the function achieves its extreme values on an interval at these points. That's something we are often interested in -- when is a function at its peak, or valley?

We can see, however, that the slope is perfectly well defined everywhere for this function (with the possible exception of the end points, where the graph disappears, and we won't have limits from left and right). Now let's see how to draw a rough approximation to the derivative function in this case.

How well can you recognize derivatives and the functions that give rise to them? Let's try #3, p. 122.

Now I'd like to use the definition of the derivative function,

\[ f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

to determine the derivative functions of these important functions:

1. Constant functions: $f(x)=c$
2. Linear functions: $f(x)=mx+b$
3. Quadratic functions: $f(x)=ax^2+bx+c$

4. An important application of the tangent line

If a function's derivative is another function, does that function have a derivative?

The derivative of the derivative of a function is called the second derivatives of the function. And how do we interpret these "higher derivatives" in the context of a motion?

Let's think of a quadratic motion, e.g. the motion of an eraser thrown across the room. Let s be the height of the eraser:

$s(t)=at^2+bt+c$

Each of the coefficients has an important, intuitive role to play:

• $c$ is the height at time $t=0$;
• $b$ is the rate of change in height at time $t=0$;
• $2a$ is the acceleration (due to gravity) of the height.

\[ f^\prime(x) = \frac{dy}{dx} = \frac{d}{dx}\left(f(x)\right)=\left(f(x)\right)'=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

There are several different ways of writing the derivative, and you need to get used to them. The third form reminds us that differentiation is itself a function: it takes a function in its domain and returns another function -- the derivative.

• #13, p. 136
• #22, p. 136
• #48, p. 137
• #56, p. 137