- Quiz today at the end of the hour.
- You have a homework assignment due today.
- No new homework assigned today: I'll assign some 2.1 problems on Friday. Remember that we'll meet in the computer lab 306 on Friday.
Once we're done with continuity, we'll move along to chapter 2 and the definition of the derivative -- only you've already seen it!:)
I want to do one squeeze theorem problem, however: #59, p. 71. It's quite an interesting function, and it ties in well with our topic of continuity. Actually, it should be "anti-continuity!".
Some things that you need to know about rational and irrational numbers:
- A rational number is a ratio of integers;
- An irrational number isn't! $\pi$, $\sqrt{2}$, $e$ are some famous irrational numbers.
- There are more irrational numbers than rational numbers. Both sets are infinite, but the irrationals form a bigger infinite set.(!)
- Between every two irrationals there is a rational; between every two rationals is an irrational.
- Section 1.8: Continuity
- What is the difference between continuous and discontinuous things?
- Missing days in calculus class?
- A sidewalk?
- Coffee poured into a cup?
- Global Temperature?
- How does a function sound?
- Definition: continuity at a point
Note: three things have to happen:
- The limit of $f$ exists at $a$,
- The function value $f(a)$ exists at $a$, and
- The two values are equal.
is discontinuous at
There are various kinds of discontinuity (which we've already seen):
- Removable discontinuities (e.g. holes)
- Jump discontinuities
- Infinite discontinuities (vertical asymptotes)
- Even rational/irrational discontinuities so ugly that a function is continuous at only a single point! (#59, p. 71)
- Maybe a better intuitive definition: a function is continuous
on an interval if its graph can be traced on
that interval without lifting the pencil from the paper.
- Many of the functions we've considered so far satisfy this, although not all do: consider the "holy function"
This function has a limit at zero (-.5), but is not defined there. Hence it is not continuous at $x=0$.
- Since continuity is wrapped up with limits, we have the same kinds
of results that we did in relation to limits:
- We define one-sided continuity, for example: $f$ is
continuous from the left at $x=a$ if
$\lim_{x\rightarrow{a^-}}f(x)=f(a)$ - we have sum laws, product, and quotient laws. We've
already used these to demonstrate that polynomials are
continuous on all real numbers:
- We define one-sided continuity, for example: $f$ is
continuous from the left at $x=a$ if
- Classes of functions that are continuous on their domains:
- Polynomials
- Rational functions: (ratios of polynomials)
- Trigonometric functions: sine, cosine, tangent
Obviously it's not possible to draw the graph of the tangent function without lifting one's pencil from the paper: but, on every interval within its domain, it can be done. Tangent is continuous on its domain.
- Power functions: $f(x)=x^{n}$
- Root functions: $f(x)=x^{1/n}$
- Exponential functions: $f(x)=b^x$
- For all these functions one can evaluate limits using the
so-called
"substitution method": simply plug in for
.
Now that's the way to do limits! (So life gets really good when functions are continuous.)
- An interesting new function (the greatest integer function)
has an infinite number of discontinuities on its domain (Example 10,
p. 68). For you computer science types, this function is often called
the floor function -- can you see why? How would the
ceiling function differ?
(This picture is a little deceiving (actually a lot deceiving!): let's have a look with Mathematica.)
- An important theorem (p. 88), RE composite functions (remember that I told you how important compositions are? here's one place they show up....):
Roughly: A composition of continuous functions is continuous.
Let $F(x)=f(g(x))$ be a composite function.
If $g$ is continuous at $x=c$ and $f$ is continuous at $g(c)$ then
$F(x)$ is continuous at
.
- What is the difference between continuous and discontinuous things?
- Examples: pp. 90-93, with Mathematica
- #3
- #10
- #12
- #19
- #23
- #36
- #46
- The Intermediate Value Theorem is an important result of continuity:
- Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.
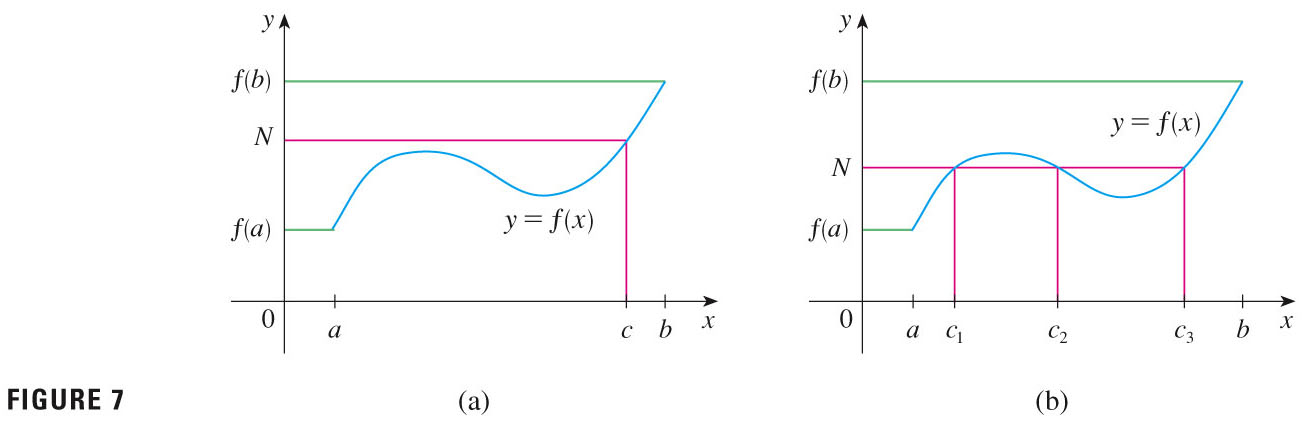
This figure illustrates that there may be multiple values $c$.
- Example: pp. 93, #69
- Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.
- We lead into the derivatives by discussing secants, tangents, limits.
Secant line slopes thus represent an approximation to the slope of the tangent line: we think of them as an "average change" over an interval, whereas the tangent line is the "change" over a point!
The secant line slopes represent an average rate of change of a function, whereas the tangent line slopes represent an instantaneous rate of change of the function.
But it's all about slopes! That's made clear by the important equations on p. 104 and 105.
These are tangent lines (places where a line osculates a curve):
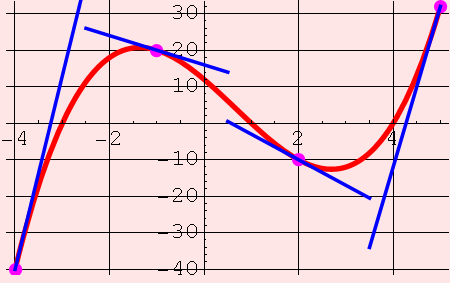
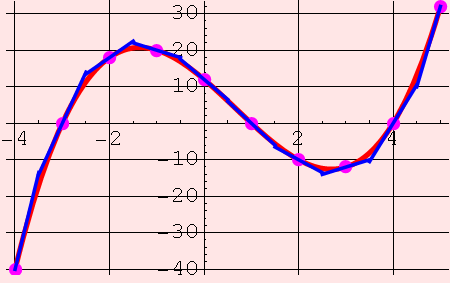
These are "rates of change" of the function f. What does that mean? The thing that tells you how fast a function is changing is its slope, isn't it? If a function is constant, then it's not changing at all. If the slope is steep (either up or down), then the function's values are changing dramatically and quickly.
The rate of change is dictated by the slope. So it should come as no surprise that the derivative of a function at a point is the same as the slope of the tangent line at a point:
We can approximate tangent lines with secant lines:
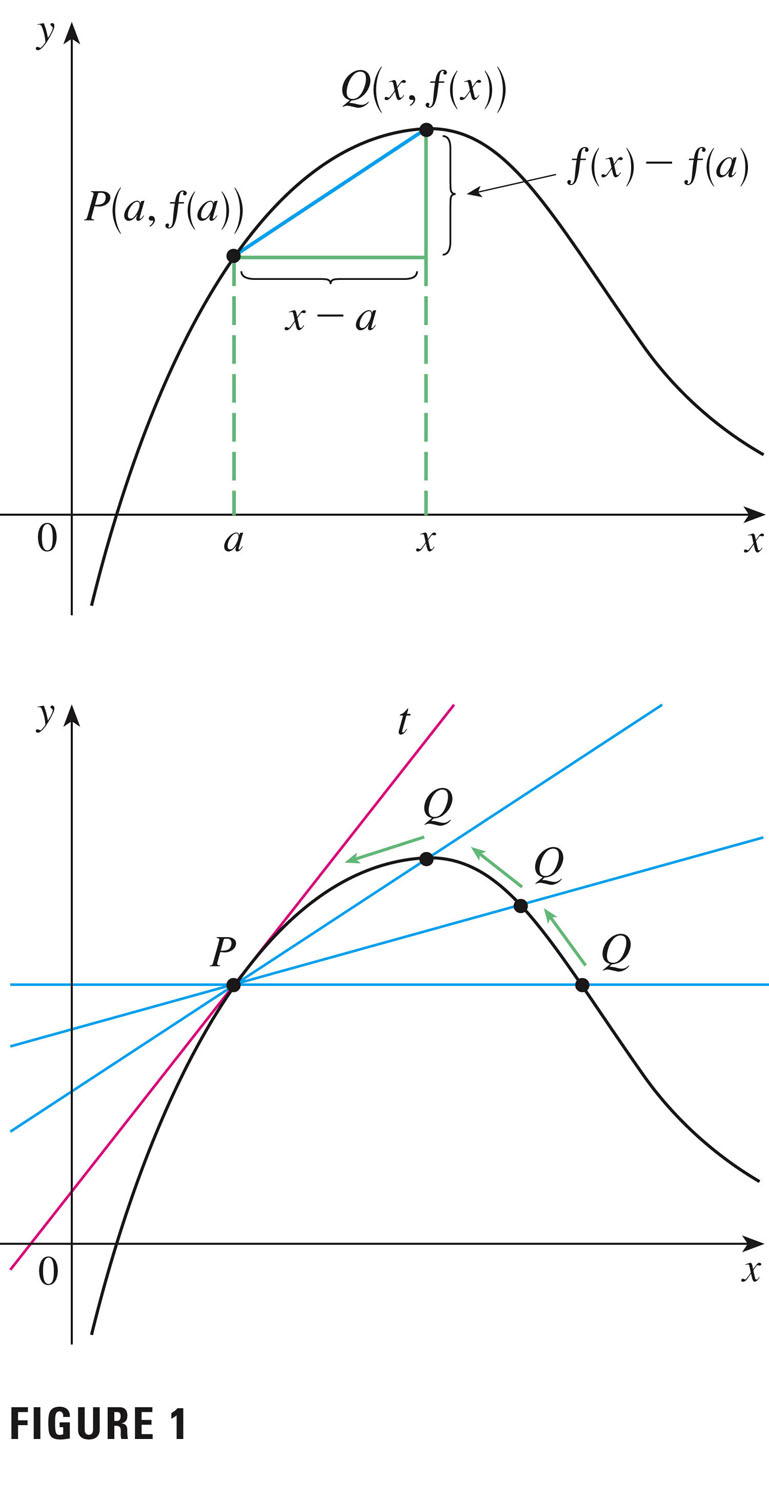
The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment (the slope of a secant line), $\frac{f(x)-f(a)}{x-a}$ This is an average rate of change in f over a finite interval.
In the limit, this average rate of change becomes an instantaneous rate of change:
$m=\lim_{x\to{a}}\frac{f(x)-f(a)}{x-a}$ 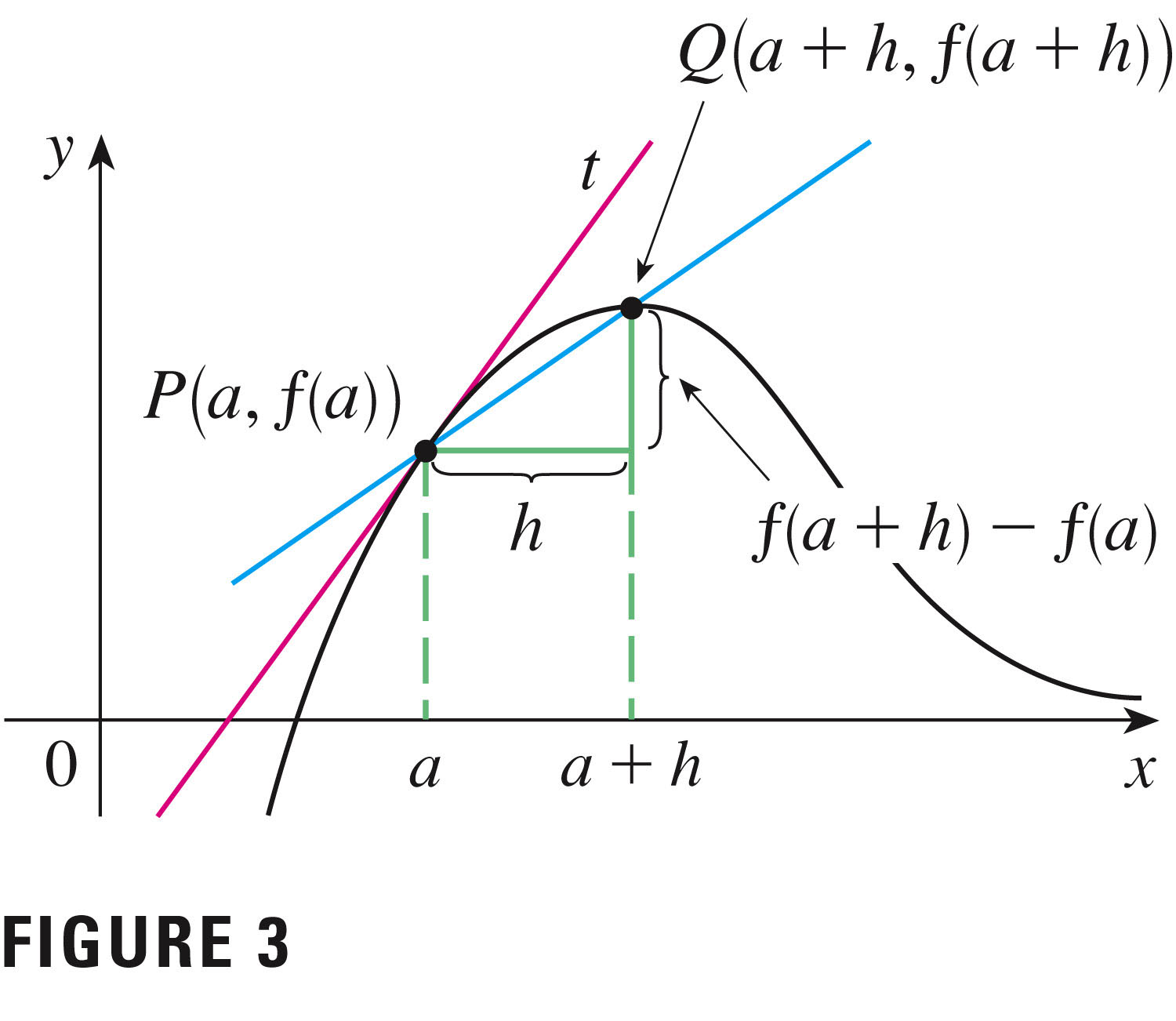
Here's an alternative notation for the slope: The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment,
$\frac{f(a+h)-f(a)}{h}$ In the limit, this is
$m=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ which I call the most important definition in calculus.
- Definition of the derivative at a point: well, it's just a slope, isn't it:
$f^\prime(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}$
The most important definition in calculus! (I just can't say it enough!)
Now let's look at some problems, and see how this concept is connected to real-world problems.
- #3, pp. 110
- #11, pp. 111
- #13, pp. 111
- #45, pp. 112
- #51, pp. 113