- Your homework is (left at home - sorry!). Graded
- 4, p. 567
- 16
- 32
- And now for something completely different....
A good introduction to parametric curves is given by ballistics. If we shoot a bullet straight from shoulder height into the air with speed v horizontally, and we neglect all forces but gravity, then the bullet will trace out a parabola (some bullets are larger than others: start this one from the top of the parabola):
Now how might we characterize the path of the bullet? The answer is a parametric curve, of the form C(t)=(x(t), y(t)).
or If we wish, we can solve for t in the equation for x and use that to eliminate the parameter t from the equation for y, hence getting an equation for the parabola traced out: According to this parameterization, where is the "bullet" at time t=0? In which direction is the motion occuring -- left to right, or right to left? (You probably have a parametric graphing mode on your calculator -- you might like to try it out.)
Orbits of planets in the heavens (minute 11:45 or so), movements of ants on a hill, a robotic arm in an assembly plant: all these can be described by parametric curves.
- A couple of famous examples involving the cycloid:
- The Brachistochrone Problem (1696, solved by Newton in a single day after he heard the challenge)
- The Tautochrone Problem (1673)
- Parametrizing a line:
- Parametrizing a circle:
- There are two distinctively different kinds of derivatives that
we're going to have to consider here:
- There are the time-derivatives, which give us the actual
speeds of the "particles" as they zip along in time. For the bullet,
the speed will be
- There is the slope of the tangent line to the curve traced
out by the particle, which one can obtain using the time-derivatives:
- There are the time-derivatives, which give us the actual
speeds of the "particles" as they zip along in time. For the bullet,
the speed will be
- One of the most important applications of parametric curves is in
the Bezier curve section. There are lots of important instances
where we need to be able to design custom curves, and this is one of
the most common ways of creating them. For example, you can use them to
create your own "sigmac", using control points. (I had all my
students create their own in numerical analysis.)
- One of the most important observations about parametric equations
is that we can use them to trace out curves which are not traditional
functions
.
- Examples:
- Parametrics occur in differential equations
- #24, p. 666 (and trace out the motion)
- #1, p. 665
- #3
- #7
- #15
- We start with the the chain rule, and the derivative
dy/dx. We must express this derivative in terms of time, which
is the actual independent variable in parametric curves:
- Tangent lines and Arc Length
-
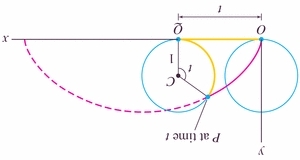
Suppose a particle has followed the parametric curve
- Examples:
- #1, p. 675
- #3 (we need a point and a slope, dy/dx)
- #20 (where is dy/dx=0 or
?)
- #41
: then we
can compute how far the particle has travelled during the
interval 
easily
using the dirt formula, 
(in its modified
form 
).
In this case, the rate is just the speed. So we compute the integral
This is actually just a re-expression of the arc length formula:
and
.
But arc length may be different from the distance the particle travelled: a particle can revisit many sections of the curve y(x) -- so once again we need to be careful to distinguish between the independent variable of interest (whether x or t).
Let's calculate how far a particle travelled when parameterized by
and 
, with 
What happens to our integral if we double the time interval?
- Examples: