- Reminder: turn off your rectangles.
- You have a quiz on Friday, over sections 1.4 and 1.5.
- Your first homework to turn in is also due Friday. See the assignment page.
- You have a new assignment for section 1.5.
- Gil Strang's "Central Idea of Calculus":
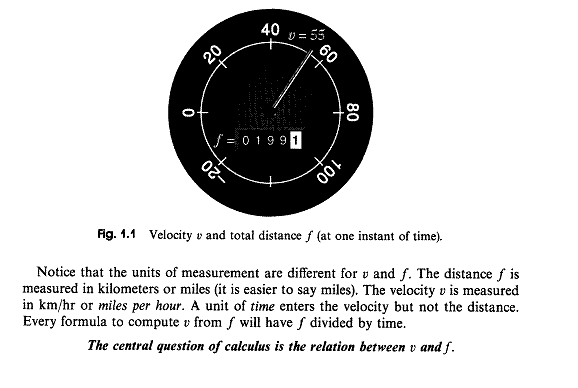
The velocity part is the derivative; the total distance part is the integral. In this course, we're focused on derivatives, hence the velocity. In particular, we speak of "instantaneous velocity" -- the velocity at a single point in time.
That's what your speedometer is showing.
- Let's look back at some examples from 1.4, using Mathematica.
We begin with p. 50, and Figure 1: this figure presents us with the basic idea.

limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$.
Questions:
- In the figure what is $a$, and what is $L$?
- To what class of functions does $f$ belong?
- Do limits even care about what happens exactly at $a$?
We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if \[ \lim_{x \to a^-}f(x) = L \] and \[ \lim_{x \to a^+}f(x) = L \] then \[ \lim_{x \to a}f(x) = L \]
Let's check out some examples from section 1.5, and check out not only the limits, but also what dangers lurk, even when we have very good technology. You can't always trust your calculator; trust your brain first.
Finally we'll look at a few problems from the text (pp. 59--).