- I still haven't received all of your
hurt/health papers, which I'd like to put on-line. Thanks to those who've
gotten them to me.
- I also need the intervention papers/presentations provided
electronically. I'll finish grading those once I've received these.
- Please revise your questions, and send them back so that I can
post those. If you need to discuss with me, please do!
- Please hand in your simple graphs on five vertices.
Question of the Day (slight reprise):
- Definition of a graph: a graph is
- a collection of vertices,
- a collection of edges, and
- a set of rules, one for each edge, telling how each edge is connected to its pair of vertices.
- Some properties of graphs:
- The degree of a vertex is the number of edges
coming into it.
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs. We can move vertices around, rotate graphs, etc. --
so long as we don't change their connectivity, it's the same graph.
- Last time we focused on simple graphs: a graph is simple if
it doesn't have any loops (edges connected from a vertix to itself), or
multiple edges with the same two vertices.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Duality allows us to simplify our work. One graph is dual to
another if the two have no edges in common, but combine to form the
complete graph. They complement each other perfectly.
To find the dual $\overline{G}$ of a graph $G$, use the following scheme:
- Draw the vertices of the graph $G$.
- If two vertices in $G$ are unconnected, connect them in $\overline{G}$.
- If two vertices in $G$ are connected, don't connect them in $\overline{G}$.
- The degree of a vertex is the number of edges
coming into it.
- Last time we drew all the simple graphs with three and four
vertices, organized by number of edges. And we used duality to do only "half" the work.
We can use graphs to organize our work with graphs: simple graphcs with four vertices. Could we have done it better, to illustrate duality, for example?
For homework I asked you to draw all simple graphs with five vertices: here they are, organized by duality.
- Planar graphs are graphs that can be drawn such that no two edges
intersect.
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
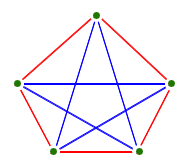
- We can show that the complete graph with four vertices is planar.
- Why isn't the five graph planar? What happens?
- The three utilities and three houses graph is not planar, either:

- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:

- We may find ourselves using graphs to understand the social
dynamics of Newport. We might start by considering adjacency in
Newport. Each block group is a vertex, and an edge exists between
vertices if they are adjacent.
- Now let's consider an unusual application of graphs to the study of social dynamics
-- in particular to decide when social situations are stable.
In "The Enemy of My Enemy", Steven Strogatz considers negative numbers and graphs.
- The focus of this reading is negative numbers. The
Indians (of Asia!) also put negative numbers on a firm
foundation (as well as zero), in about the 6th century
AD.
"...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says Strogatz).
- One of the confusing aspects of negative numbers
from Strogatz's perspective is that the product of two
negative numbers is a positive number. The story about
the two linguists is priceless.
- But then Strogatz goes on to use the context of
social interactions (negative and positive) to discuss
how we maintain stable relationships.
And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be "equal" to the other interaction: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.
Furthermore, if two interactions are negative, then the third must be positive -- (-1)(-1)=(+1) -- a negative times a negative equals a positive.
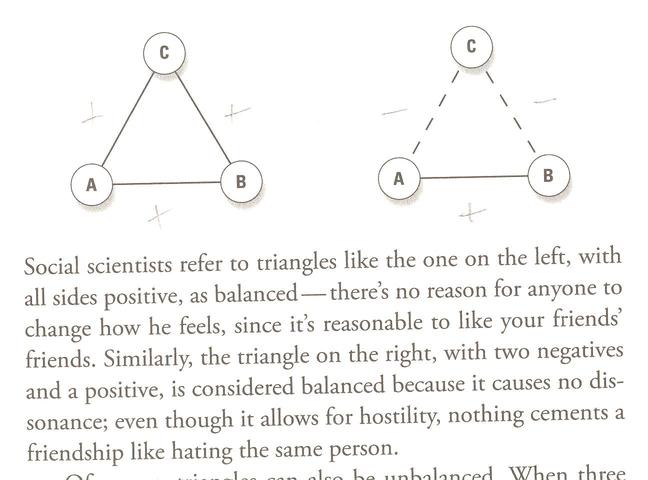
Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".
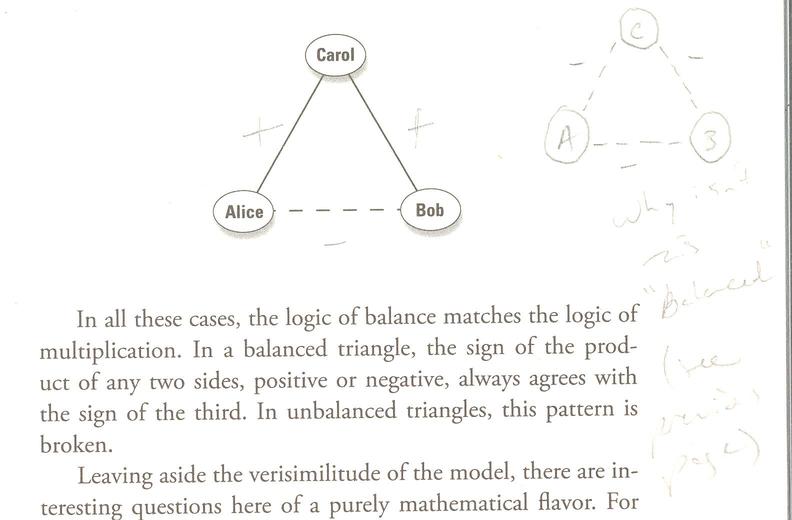
The following (two) graphs are unbalanced:
Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."
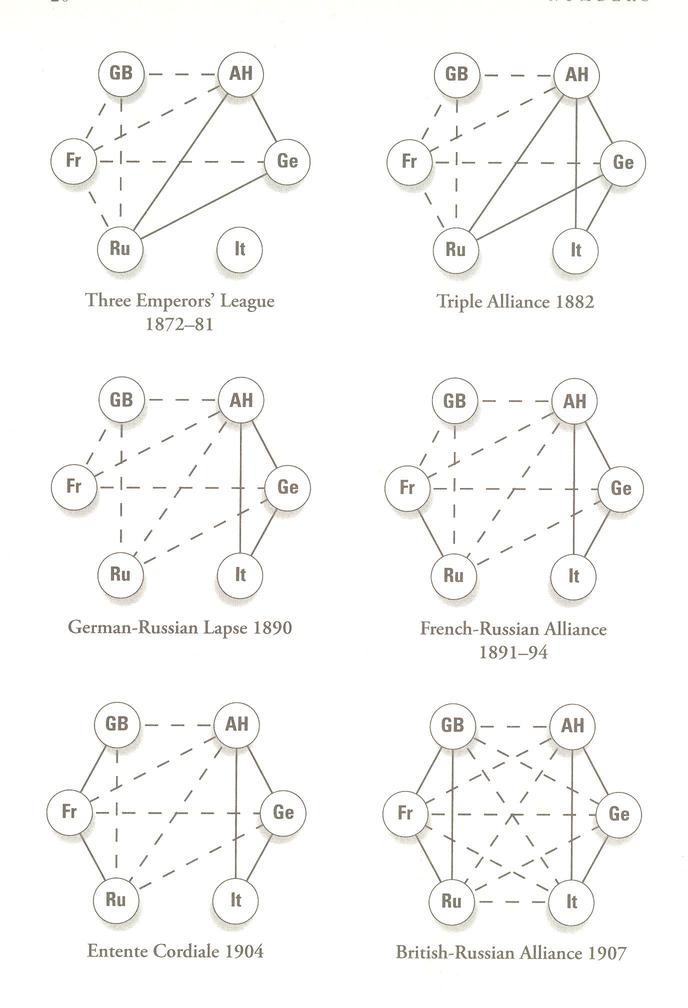
The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."
- The focus of this reading is negative numbers. The
Indians (of Asia!) also put negative numbers on a firm
foundation (as well as zero), in about the 6th century
AD.
- Now we turn to Google.... Chapter 24: Untangling the Web (directed graphs) -- p. 191.
This section describes how Google uses the "Pagerank" algorithm to determine the importance or value of a webpage (and hence where it falls in the search results for a particular topic).
Strogatz asserts that "A page is good if good pages link to it," then discusses this self-referential definition of a good page. (p. 193)
The question is this: who decides which pages are good in the first place? As Strogatz describes, the network does!
"Worrying about content turned out to be an impractical way to rank webpages." (p. 192) We left people vote with their feet (or rather, with their clicks.)
Graphs provide a useful way of illustrating how pages interact. If there's a link between two pages, then a directed arrow indicates it. Here's the graph of the "toy web" Strogatz considers, with the final rankings:
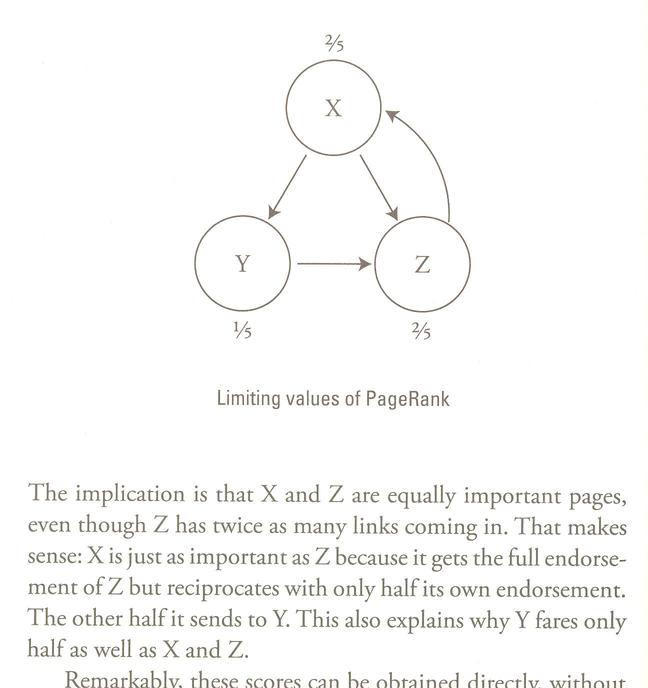
He justifies this ranking in a series of graphs, and a set of equations on page 195. Let's see how these equations work (we'll use this Excel spreadsheet).
He starts by assigning all pages equal weight: in this case, if we call the total weight 1, each page starts with weight 1/3.
Notice that I've written the equations with an index,
, rather than with the primes. That's because we keep updating the values to get them at the
stage, and we update based on the previous stage's (
) values.
We just "do it again", over and over....
This "systems of equations" is an example from the field of mathematics called "linear algebra". If you loved algebra, wait -- there's more!:)
Now here's the big question: How do you improve the value of your website, given that you understand the PageRank algorithm?
Side note: Google's plan to prioritize facts ticks off climate deniers: The strategy isn't being implemented yet, but the paper presented a method for adapting algorithms such that they would generate a "Knowledge-Based Trust" score for every page. To do this, the algorithm would pick out statements and compare them with Google's Knowledge Vault, a database of facts. It would also attempt to assess the trustworthiness of sources -- for example, a reputable news site versus a newly created WordPress blog....